개요
기계 학습 및 자연어 처리 분야에서 토픽이라는 문서 집합의 추상적인 주제를 발견하기 위한 통계적 모델 중 하나로, 텍스트 본문의 숨겨진 의미 구조를 발견하기 위해 사용되는 텍스트 마이닝 기법인 topic modeling에 대해 알아보자.
1. 잠재 의미 분석(Latent Semantic Analysis, LSA)
LSA는 정확히 토픽 모델링을 위해 최적화 된 알고리즘은 아니지만, 토픽 모델링이라는 분야에 아이디어를 제공한 알고리즘이라 볼 수 있다. 이에 토픽 모델링 알고리즘인 LDA(LSA의 단점 개선한 알고리즘. 이후에 설명)에 앞서 배워보도록 하자.
BoW에 기반한 것들은 단어의 의미를 고려하지 못한다는 단점이 있다. 이를 위한 대안으로 잠재 의미 분석(LSA)이란 방법이 있다. 이 방법을 이해하기 위해서는 선형대수학의 특이값 분해(Singular Value Decomposition, SVD)를 이해할 필요가 있다.
1.1 특이값 분해(Singular Value Decomposition, SVD)
시작하기 앞서, 여기서의 특이값 분해(Singular Value Decomposition, SVD)는 실수 벡터 공간에 한정하여 내용을 설명함을 명시한다. SVD란 A가 m × n 행렬일 때, 다음과 같이 3개의 행렬의 곱으로 분해(decomposition)하는 것을 말한다
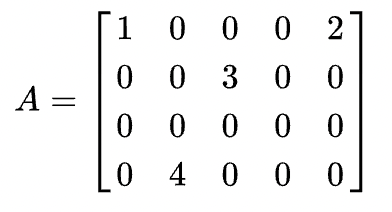

그림에서 $V^*$는 위키피디아에서 V의 켤레전치라 표현한다. 여기서 $V^T$와 같다고 보면된다.
$A = U\Sigma V^T$
여기서 각 3개의 행렬은 다음과 같은 조건을 만족한다.
- $U : m \times m $ 직교행렬(orthogonal matrix) ($AA^T = U(\Sigma\Sigma^T)U^T$)
- $V : n \times n $ 직교행렬(orthogonal matrix) ($A^TA = V(\Sigma\Sigma^T)V^T$)
- $\Sigma : m \times n $ 직사각 대각 행렬(diagonal matrix)
➕ 용어 정리
- 전치 행렬(Transposed Matrix)
원래 행렬에서 행과 열을 바꾼행렬. 기호는 기존 행렬 표현 우측 위에 T를 붙인다.
$$ M = \begin{bmatrix}1 & 2 \\ 3 & 4 \\ 5 & 6 \\ \end{bmatrix} M^T = \begin{bmatrix}1 & 3 & 5 \\ 2 & 4 & 6 \\ \end{bmatrix} $$ - 단위 행렬(Identity Matrix)
주 대각선의 요소만 1이고 나머진 0인 정사각 행렬. 어떤 행렬에 곱하든 자기 자신이 나옴 ex) $A \times I=A$
$$ I = \begin{bmatrix}1 & 0 \\ 0 & 1 \\ \end{bmatrix} I = \begin{bmatrix}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{bmatrix} $$ - 역행렬(Inverse Matrix)
행렬 A와 어떤 행렬을 곱했을 때 단위 행렬이 나온다면, 이때의 어떤 행렬을 $A$의 역행렬 $A^{-1}$ 이라 표현한다.
$A \times A^{-1} = I$
$$ \begin{bmatrix}1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \\ \end{bmatrix} \times \begin{bmatrix} \qquad \\ ? \\ \qquad \\ \end{bmatrix} = \begin{bmatrix}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{bmatrix} $$ - 직교 행렬(Orthogonal Matrix)
실수 $n \times n$ 행렬 $A$에 대하여 $A \times A^{-1} = I$를 만족하면서 $A^{-1} \times A = I$를 만족하는 행렬$A$를 직교행렬이라 한다. 또한 직교행렬은 역행렬의 정의를 통해 $A^T = A^{-1}$를 만족한다. - 대각 행렬(Diagonal Matrix)
주 대각선의 원소를 제외한 원소가 모두 0인 행렬을 말한다. 주 대각선의 원소가 a라고 한다면 3 x 3 행렬이라면 아래와 같이 표현할 수 있다.
$$\Sigma = \begin{bmatrix}a & 0 & 0 \\ 0 & a & 0 \\ 0 & 0 & a \\ \end{bmatrix}$$
직사각 행렬이 될 경우 잘 보아야 헷갈리지 않는다. m x n 행렬일 때 m > n인 경우(행이 열보다 클 때)이다
$$\Sigma = \begin{bmatrix}a & 0 & 0 \\ 0 & a & 0 \\ 0 & 0 & a \\ 0 & 0 & 0 \\ \end{bmatrix}$$
m < n인 경우(열이 행보다 클 때)이다
$$\Sigma = \begin{bmatrix}a & 0 & 0 & 0 \\ 0 & a & 0 & 0 \\ 0 & 0 & a & 0 \\ \end{bmatrix}$$
SVD를 통해 나온 대각 행렬은 추가적인 성질을 가지는데, 주 대각원소를 행렬 A의 특이값(singular value)라고 하며, 이를 $\sigma_1, \sigma_2 , ... ,\sigma_r$ 이라 표현한다면 특이값 $\sigma_1, \sigma_2 , ... ,\sigma_r$은 내림차순으로 정렬되어 있다는 특징을 가진다. 즉 다음 행의 값은 그 전 행의 값보다 클 수 없다는 것이다.
$$\Sigma = \begin{bmatrix}12.4 & 0 & 0 \\ 0 & 9.5 & 0 \\ 0 & 0 & 1.3 \\ \end{bmatrix}$$
간단하게 정리하자면 하나의 행렬 ex) A를 3가지 행렬 $U\Sigma V^T$으로 분해할 수 있고, 그렇게 얻은 대각 행렬 $\Sigma$의 원소들은 A 행렬의 특이값들이 된다는 것 같다.
수학적으로 더욱 자세히 알고 싶다면 https://angeloyeo.github.io/2019/08/01/SVD.html 이런 곳을 참고해보는 건 어떨까.
1.2 절단된 SVD (Truncated SVD)
위에서 설명한 SVD를 full SVD라고 한다. 하지만 LSA의 경우 full SVD에서 나온 3개의 행렬에서 일부 벡터들을 삭제시킨 절단된 SVD(truncated SVD)를 사용하게 된다.
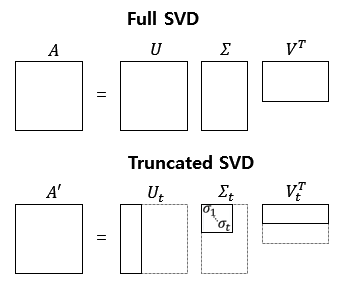
절단을 하면 대각 행렬 $\Sigma$의 원소의 값 중에서 상위값 $t$개만 남게 된다. 절단된 SVD를 수행하면 값의 손실이 일어난다. 왜 절단된 것을 사용하는가? 노이즈에 영향을 받을 수 있기 때문이다. 그래서 $t$를 하이퍼파라미터로 사용한다. 결과적으로 $t$를 크게 잡으면 기존 행렬 A로 부터 다양한 의미를 가져갈 수 있지만, $t$를 작게 잡아야 노이즈를 제거할 수 있다. 게다가 차원이 줄어들어 계산 비용 또한 낮아진다.
1.3 잠재 의미 분석(Latent Semantic Analysis, LSA)
이것을 사용하게된 배경부터 다시 생각해보자. 기존의 DTM이나 TF-IDF행렬은 단어의 의미를 전혀 고려하지 못한다는 단점을 갖고 있었다. LSA는 기본적으로 DTM이나, TF-IDF 행렬에 절단된 SVD(truncated SVD)를 사용하여 차원을 축소시키고, 단어들의 잠재적인 의미를 끌어낸다는 아이디어를 갖고 있다.
그래서 어떻게 코드로 구현될까. 어서 실습해보자. 아, numpy와 함께. (pip install numpy 필수!)
import numpy as np
A=np.array([[0,0,0,1,0,1,1,0,0],
[0,0,0,1,1,0,1,0,0],
[0,1,1,0,2,0,0,0,0],
[1,0,0,0,0,0,0,1,1]])
np.shape(A) # (4, 9)DTM 행렬 A를 예를 들어보겠다. shape을 통해 4 x 9 인 행렬임을 알 수 있다. 이 행렬을 full SVD를 수행해보자.
U, s, VT = np.linalg.svd(A, full_matrices = True)대각행렬 $\Sigma$ 를 s라고 하고, $V^T$ 를 VT라 한다면 코드 한줄로 SVD를 수행할 수 있다.
특이한 점은 numpy의 linalg.svd()는 분해 결과로 대각 행렬이 아니라, 특이값의 리스트로 반환한다. 게다가 내림차순을 보이는 것을 확인할 수 있다.
print(s.round(2)) # [2.69 2.05 1.73 0.77]
np.shape(s) # (4, )
# 행렬로 바꿔주기
S = np.zeros((4, 9)) # 대각 행렬의 크기인 4 x 9의 임의의 행렬 생성
S[:4, :4] = np.diag(s) # 특이값을 대각행렬에 삽입
print(S.round(2))
np.shape(S) # (4,9)이제 t를 2로 한 SVD를 해보자. 위에서 구한 값에서 행과 열을 맞춰줌으로 제거할 수 있다.
S=S[:2,:2]
U=U[:,:2]
VT=VT[:2,:]이렇게 자른 행렬을 다시 붙여서 $A'$ 행렬을 만들어 원래 행렬 $A$와 비교해보자.
A_prime=np.dot(np.dot(U,S), VT)
print(A)
print(A_prime.round(2))[[0 0 0 1 0 1 1 0 0]
[0 0 0 1 1 0 1 0 0]
[0 1 1 0 2 0 0 0 0]
[1 0 0 0 0 0 0 1 1]]
[[ 0. -0.17 -0.17 1.08 0.12 0.62 1.08 -0. -0. ]
[ 0. 0.2 0.2 0.91 0.86 0.45 0.91 0. 0. ]
[ 0. 0.93 0.93 0.03 2.05 -0.17 0.03 0. 0. ]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. ]]대체적으로 기존에 0인 값들은 0에 가까운 값이 나오고, 1인 값들은 1에 가까운 값이 나오는 것을 볼 수 있다. 또한 값이 제대로 복구되지 않은 구간도 존재하는 것 같다. 이것들이 대체 무슨 의미를 가지고 있을까?
- 축소된 U는 (4 x 2)의 크기를 가지는데, 이는 (문서의 개수 x 토픽의 수 t) 의 크기라고 할 수 있다. 4개의 문서 각각을 2개의 값으로 표현한다. 즉, U의 각 행은 잠재 의미를 표현하기 위한 수치화 된 각각의 문서 벡터라고 볼 수 있다.
- 같은 맥락으로 축소된 VT는 토픽의 수와 단어의 개수 트기이다. 각 열은 잠재의미를 표현하기 위해 수치화된 각각의 단어 벡터라고 볼 수 있다.
➕ 내가 받아 드린 바로는, DTM을 기준으로 설명하자면,
- 하나로된 단어와 문서행렬($A$= d(문서수) x w(단어수) 행렬)을
- 특이값으로 분해($A= U \Sigma V^T$)하여 토픽으로 차원을 줄이면($\Sigma $= t x t 행렬로 줄임)
- 문서와 토픽간의 행렬($U \times \Sigma = U_t$= d x t) / 토픽과 단어간의 행렬($\Sigma \times V^T = V^T_t$= t x w)로 만듬
- 이렇게 나온 $U_t$, $V^T_t$ 행렬을 이용해서 각 문서(또는 단어) 사이의 코사인 유사도와 같이 유사도를 구할 수 있다.
이렇게 결과로 나온 문서 벡터와 단어 벡터를 통해 다른 문서의 유사도, 다른 단어의 유사도, 단어(쿼리)로부터 문서의 유사도를 구하는 것들이 가능해진다.
이 영상을 보면 이해하는데 도움이 될까 싶어서 링크를 달아둔다. https://www.youtube.com/watch?v=GVPTGq53H5I
scikit-learn 을 이용하여 tf-idf나 dtm 행렬을 인풋 (ex. 밑에 코드에선 X)으로 truncated SVD를 쉽게 구해볼 수 있다.
from sklearn.decomposition import TruncatedSVD
svd_model = TruncatedSVD(n_components=20, algorithm='randomized', n_iter=100, random_state=122)
svd_model.fit(X)
len(svd_model.components_)n_components는 토픽의 수(이전 설명의 t)이고, svd_model.components_는 VT 행렬에 해당한다.
이렇게 추출된 행렬을 사용하여 예를 들어 특정 토픽에 가장 큰 값을 가지는 단어를 찾아낼 수 있다.
토픽에 행이므로 한 행의 요소들 중에 제일 높은 값을 가지는 인덱스를 찾으면 단어를 알 수 있다.
1.4 LSA의 장단점
LSA는 쉽고 빠르게 구현이 가능할 뿐만 아니라 단어의 잠재적인 의미를 이끌어낼 수 있어 문서의 유사도 계산등에서 좋은 성능을 보여준다는 장점을 갖고 있다. 하지만 SVD의 특성상 새로운 정보에 대해 업데이트가 어렵다. 처음부터 다시 계산해야 하기 때문이다.
2. 잠재 디리클레 할당(Latent Dirichlet Allocation, LDA)
토픽 모델링은 문서의 집합에서 토픽을 찾아내는 프로세스를 말한다. 문서들은 토픽들의 혼합으로 구성되어져 있으며, 토픽들은 확률 분포에 기반하여 단어들을 생성한다고 가정한다. 데이터가 주어지면 LDA는 문서가 생성되던 과정을 역추척한다. 이게 무슨 말일까?
2.1 개요
우선 내부 메커니즘을 이해하기 전 LDA를 일종의 블랙 박스로 보고 LDA에 문서 집합을 입력하면, 어떤 결과를 보여주는지 다음 예를 보고 확인해보자.
문서1 : 저는 사과랑 바나나를 먹어요
문서2 : 우리는 귀여운 강아지가 좋아요
문서3 : 저의 깜찍하고 귀여운 강아지가 바나나를 먹어요위와 같에 3개의 문서가 있다고 하자. LDA를 수행할 때 문서 집합에서 토픽이 몇 개가 존재할지 가정하는 것은 사용자가 해야 할 일이다. 여기서는 LDA에 2개의 토픽을 찾으라고 가정하자.
# 각 문서의 토픽 분포
문서1 : 토픽 A 100%
문서2 : 토픽 B 100%
문서3 : 토픽 B 60%, 토픽 A 40%
# 각 토픽의 단어 분포
토픽A : 사과 20%, 바나나 40%, 먹어요 40%, 귀여운 0%, 강아지 0%, 깜찍하고 0%, 좋아요 0%
토픽B : 사과 0%, 바나나 0%, 먹어요 0%, 귀여운 33%, 강아지 33%, 깜찍하고 16%, 좋아요 16%LDA는 토픽의 제목을 정해주지 않지만, 이 시점에서 알고리즘의 사용자는 위 결과로부터 두 토픽이 각각 과일에 대한/강아지에 대한 토픽이라고 판단해볼 수 있다. 이거까지만 봐서는 솔직히 LSA와 LDA의 차이를 잘 모르겠다.
2.2 LDA의 가정
LDA는 문서의 집합으로부터 어떤 토픽이 존재하는지를 알아내기 위한 알고리즘이다. 앞서 배운 빈도수 기반의 표현 방법인 BoW의 행렬 DTM 또는 TF-IDF 행렬을 입력으로 하는데, 이로부터 알 수 있는 사실은 단어의 순서는 신경쓰지 않겠다는 점이다. 그리고 문서들로부터 토픽을 뽑아내기 위해 모든 문서 하나하나가 작성될 때 그 문서의 작성자는 이러한 생각을 했다. '나는 이 문서를 작성하기 위해서 이런 주제들을 넣을거고, 이런 주제들을 위해 이런 단어를 넣을 거야.' 아직 뭔소린지 모르겠다. 구체적으로 살펴보자.
문서에 사용할 단어의 개수 N을 정한다. ex) 5개 단어 정한다.
문서에 사용할 토픽의 혼합을 확률 분포에 기반하여 결정한다.
- 위 예제 같이 토픽이 2개라고 했을 때, 강아지 토픽을 60%, 과일 토픽을 40%와 같이 선택할 수 있다.
문서에 사용할 각 단어를 (아래와 같이) 정합니다.
- 토픽 분포에서 토픽 T를 확률적으로 고른다.
- ex) 60% 확률로 강아지 토픽을 선택하고, 40% 확률로 과일 토픽을 선택할 수 있다.
- 선택한 토픽 T에서 단어의 출현 확률 분포에 기반해 문서에 사용할 단어를 고른다.
- ex) 강아지 토픽을 선택하였다면, 33% 확률로 강아지란 단어를 선택할 수 있다. 이제 3을 반복하면서 문서 완성.
이러한 과정을 통해 문서가 작성되었다는 가정 하에 LDA는 토픽을 뽑아내기 위하여 위 과정을 역으로 추적하는 역공학(reverse engineering)을 수행한다. 솔직히 아직도 모르겠다.
2.3 LDA 수행
위에서 나온 수행과정을 구체적으로 정리해보자.
1️⃣ 사용자는 알고리즘에게 토픽의 개수 k를 알려준다.
토픽의 개수를 알려주는 것은 사용자의 역할이다. LDA는 토픽의 개수 k를 입력받으면, k개의 토픽이 M개의 전체 문서에 걸쳐 분포되어 있다고 가정한다.
2️⃣ 모든 단어를 k개 중 하나의 토픽에 할당한다.
이제 LDA는 모든 문서의 모든 단어에 대해서 k개 중 하나의 토픽을 랜덤으로 할당한다. 이 작업이 끝나면 각 문서는 토픽을 가지며, 토픽은 단어 분포를 가지는 상태이다. 랜덤으로 할당했기에, 전부 틀린 상태다. 만약 한 단어가 한 문서에 2회 이상 등장했다면 각 단어는 서로 다른 토픽에 할당되었을 수도 있다.
3️⃣ 이제 모든 문서의 모든 단어에 대해 아래 사항을 반복한다.
- 어떤 문서의 각 단어 w는 자신은 잘못된 토픽에 할당되어져 있지만, 다른 단어들은 전부 올바른 토픽에 할당되어졌다고 가정하자. 이에 따라 단어 w는 아래 두가지 기준에 따라 토픽이 재할당된다.
- p(topic t | document d) : 문서 d의 단어들 중 토픽 t에 해당하는 단어들의 비율
- p(word w | topic t) : 각 토픽들 t에서 해당 단어 w의 분포
간단한 예제로 이해해보자.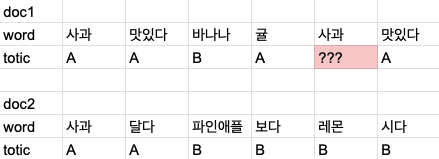
여기서 빨간색으로 칠한 사과의 토픽을 결정하려고 한다.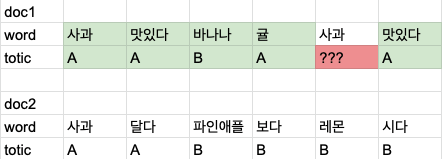
첫번째 방법은 한 문서내에 다른 단어들의 토픽 분포를 보고 결정한다. doc1에서 A의 분포가 많으므로 A 로 할당될 확률이 높다.
두번째 방법은 모든 문서에서 등장한 같은 단어의 토픽 분포를 보고 결정한다. 여기서도 다른 사과가 A인 경우가 많아서 A 로 할당할 확률이 높다고 볼 수 있다.
여기서 드는 의문점은 처음에 LDA가 각 문서들에 토픽을 할당할 때는 어떤 기준으로 진행하는지 궁금했는데, 이곳에서 본 바 처음엔 랜덤하게 할당한다고 한다. 이후 위에서 설명한 과정을 iteration을 돌면서 수정해나가는 것으로 이해했다. 자세히 알고싶다면 저 링크를 들어가보는 것을 추천한다. 난 아무것도 몰러유...😵💫
2.4 LSA 와 LDA의 차이점
- LSA : DTM을 차원 축소 하여 축소 차원에서 근접 단어들을 토픽으로 묶는다.
- LDA : 단어가 특정 토픽에 존재할 확률과 문서에 특정 토픽이 존재할 확률을 결합확률로 추정하여 토픽을 추출한다.
결국 LSA나, LDA는 단어의 순서를 고려하지 않으므로 단어들의 빈도수만을 가지고 표현한다.
reference
'python > 자연어처리' 카테고리의 다른 글
| [자연어처리 입문] 6-2. 머신러닝 이해 (0) | 2021.06.23 |
|---|---|
| [자연어처리 입문] 6-1. 머신러닝 개요 (0) | 2021.05.31 |
| [자연어처리 입문] 4. 벡터의 유사도(Vector Similarity) (0) | 2021.05.11 |
| [자연어처리 입문] 3. 카운트 기반의 단어 표현 (0) | 2021.05.05 |
| [자연어처리 입문] 2. 언어 모델(Language Model) (0) | 2021.04.13 |