개요

딥 러닝을 이용한 자연어 처리 입문

AI는 여러 의미를 포괄하고 있지만, 지금에 이르러 사람들이 말하는 AI는 바로 머신 러닝(Machine Learning)과 머신 러닝의 한 갈래인 딥 러닝(Deep Learning)을 의미한다. 스스로 규칙을 찾아내가는 머신 러닝이 새로운 프로그래밍의 패러다임이 될 것이라 말하기도 한다. 그럼 머신러닝이란 도대체 무엇인가... 시작해보자!

1. 머신러닝이란(Machine Learning)?

왜 이것이 나오게 되었는가 부터 찬찬히 살펴보자.

1.1 머신러닝이 아닌 접근 법의 한계

예를들어 '주어진 사진으로부터 고양이 사진인지 강아지 사진인지 판별하는 일' 이라는 해결 해야 할 문제가 주어졌다고 가정하자.

이미지 출처 : 사진1 사진2 사진3

이 문제를 사람이라면 구분을 잘 하겠지만, 컴퓨터가 이것을 구분하게 한다는 것은 쉽지가 않다. 전통적인 방식으로 개발자가 직접 규칙을 정의하여 프로그램을 작성한다면 다음과 같을 것이다.

def prediction(이미지파일):
    if 눈코귀가 있을 때:   
        if 근데 강아지는 아닐때
    if 털이 있고 꼬리 있을 때:
        if 다른 동물이 아닐 때
    ...
    어캐하누...
    return 결과

위의 사진에서 볼 수 있는 것처럼, 고양이 자세나 색상 등이 너무 다양해서 공통된 명확한 특징을 모두 잡아내는 것은 사실상 불가능에 가깝다고 볼 수 있다. 존재하지도 않지만, 있다해도 어떻게 저런 것을 사람이 다 일일이 정의를 하나...

그래서 이미지 인식 분야에서 특징을 잡아내기 위한 시도들이 있었다. 이미지의 shape이나 edge와 같은 것들을 찾아내서 알고리즘화 하려고 시도하고, 다른 사진 이미지가 들어오면 전반적인 상태를 비교하여 분류하려고 한 것이다. 그렇지만 여전히 공통된 명확한 특징을 찾아내는 것에 한계가 있을 수 밖에 없기에, 머신러닝이 이에 대한 해결책이 될 수 있다.

1.2 정리

간단하게 설명하자면,

• 기존의 프로그래밍이 개발자가 직접 규칙을 정의하여 input(data)을 넣어서 output(해답)을 도출했다.

Ex) input(사진) ---> fucntion(정의한 규칙 : 꼬리와 털이 있으면 고양이다.) ---> output(고양이다)

• 하지만 머신러닝은 개발한 알고리즘을 통해 만든 model에 input(data와 해답)을 넣어 규칙을 도출해낸다.

Ex) input(사진, 고양이다) ---> model(학습) ---> output(학습한 규칙 : 꼬리와 털이 있으면 고양이다.)

• 이렇게 학습한 모델은 기존 프로그래밍처럼 input으로 data가 들어온다면 해답을 예측(추론)할 수 있게 된다.

Ex) input(사진) ---> model(학습한 규칙) ---> output(고양이다)

결과적으로 머신러닝은 주어진 데이터로부터 결과를 찾는 것에 초점을 맞추는 것이 아니라, 주어진 데이터로부터 규칙성을 찾는 것에 초점이 맞추어져 있다. 주어진 데이터로부터 규칙성을 찾는 과정을 학습(training)이라고 한다.

대충 느낌은 왔으니 조금만 더 들어가 보자!

2. 머신러닝 훑어보기

머신 러닝의 특징들에 알아보자. 딥 러닝 또한 머신 러닝에 속하므로 머신러닝의 특징들은 모두 딥러닝의 특징이기도 하다.

2.1 머신 러닝 모델의 평가

모델을 학습시켰다면, 평가를 빼놓을 수가 없다. 모델을 학습시켰는데 이것이 잘된건지 아닌지 확인을 해야 사용할 수 있을지 아닐지 판단할 수 있지 않겠는가? 그래서 실제 모델을 평가하기 위해 데이터를 훈련용, 검증용, 테스트용 이렇게 세 가지로 분리하는 것이 일반적이다.

근데 훈련이랑 테스트로 한 번만 테스트하면 되지, 굳이 검증까지 넣어뒀을까 싶다. 역시 사람들이 만들어둔 것은 다 이유가 있다. 검증용 데이터는 모델의 성능을 평가하기 위한 용도가 아니라, 모델의 성능을 조정하기 위한 용도이다. 더 자세히는 과적합이 되고 있는지 판단하거나 하이퍼파라미터의 조정을 위한 용도이다.

👆 여기서 하이퍼파라미터(hyper parameter)란?

• 값에 따라서 모델의 성능에 영향을 주는 매개변수를 말한다.
• 경사하강법에서 학습률(learning rate), 딥러닝에서 은닉층의 수, 뉴런의 수, 드롭아웃 비율 등이 이에 해당한다.
• 반면, 일반 매개변수(일반 파라미터)는 가중치와 편향과 같은 학습을 통해 바뀌어져가는 변수이다.

정리하면, 하이퍼파라미터 = 사람이 정하는 변수 / 파라미터(매개변수) = 기계가 훈련을 통해 바꾸는 변수

아무튼! 훈련용 데이터로 훈련을 모두 시킨 모델은 검증용 데이터를 사용하여 정확도를 검증하며 하이퍼파라미터를 튜닝(tuning)한다. 그러면 이 모델의 매개변수는 검증용 데이터에 대해 일정 부분 최적화가 된다. 튜닝하면서 다시 훈련을 검증용 데이터를 사용했기에 검증을 아직까지 보지 못한 데이터로 하는 것이 바람직하다. 그래서 이제 테스트 데이터로 모델의 진짜 성능을 평가한다.

결과적으로 훈련 과정을 수험생으로 비유를 하자면 훈련데이터(문제집) -> 검증데이터(모의고사) -> 테스트데이터(수능) 이라고 볼 수 있다. 문제집을 쭉 풀다가 모의고사를 보고 아 유형이 이런식이구나 하면서 모의고사에 맞춰서 공부하는 것이다. 그런 다음 마지막으로 수능을 치는 것과 같이 평가를 하는 것이다. 데이터가 충분하지 않으면 이렇게 3개로 나누는 것이 힘들 것이다. 그럴 때 k-폴드 교차 검증이라는 또 다른 방법을 사용하기도 한다.

👆 K-폴드 교차검증(K-fold cross Validation)이란?

이미지 출처

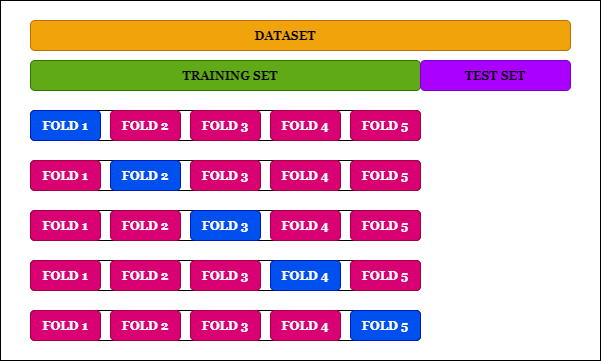
간단하게 말하자면, 테스트 세트를 제외한 데이터셋을 K개로 분할하여 나눈뒤, 검증용 데이터 부분을 바꿔가면서 각 case별로 정확도를 측정해보는 것이다. 자세히 알고싶다면 이곳을 살펴보자.

2.2 분류(Classification)와 회귀(regression)

다음으로는 머신러닝이 어떤 문제를 해결하는데 사용되는지 알아보자. 전부라고는 할 수 없지만, 머신 러닝의 많은 문제는 분류 또는 회귀 문제에 속한다.

1️⃣ 이진 분류 문제(Binary Classification)

• 이진 분류는 주어진 입력에 대해서 둘 중 하나의 답을 정하는 문제이다.
• 시험 성적에 대해 합격/불합격 또는 메일로부터 정상메일인지 스팸메일인지를 판단하는 문제 등이 이에 속한다.

2️⃣ 다중 클래스 분류(Multi-Class Classification)

• 주어진 입력에 대해 두개 이상의 정해진 선택지 중에서 답을 정하는 문제이다.
• 서점을 예로 들면 책 분야를 과학, 영어, IT, 만화 라는 레이블이 각각 붙어있는 4개의 책장이라 하면, 새 책이 입고 되면 이 책을 분야에 맞는 적절한 책장에 넣어야 한다. 이 때의 4개의 선택지를 카테고리 또는 범주 또는 클래스라고 한다. 결과적으로 주어진 입력으로부터 정해진 클래스 중 하나로 판단하는 것이다.

3️⃣ 회귀 문제(Regression)

• 회귀 문제는 분류 문제처럼 0 또는 1이나 다양한 분야가 있는 책 분류와 같이 분리된(비연속적인) 답이 결과가 아니라 연속된 값을 결과로 가진다.
• 대표적으로 시계열 데이터를 이용한 주가 예측, 생산량 예측, 지수 예측 등이 이에 속한다.

2.3 지도 학습(Supervised Learning)과 비지도 학습(Unsupervised Learning)

그러면 어떤 방법으로 학습하는지도 알아야지 않겠는가. 머신러닝은 크게 지도 학습, 비지도 학습, 강화 학습으로 나눈다. 강화 학습은 이 책에서 다루지 않으므로 두 가지만 알아보도록 하겠다.

1️⃣ 지도 학습

• 지도학습이란 레이블(Label)이라는 정답과 함께 학습하는 것을 말한다. 레이블이라는 말 외에도 y, 실제값 등으로 부르기도 한다.
• 기계는 예측값과 실제값인 차이인 오차를 줄이는 방식으로 학습을 하게 된다. 예측값은 $\hat{y}$으로 표기하기도 한다.

2️⃣ 비지도 학습

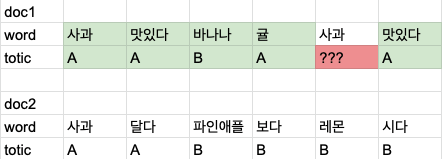
• 레이블이 없이 학습을 하는 것을 말한다. 예를들어 토픽 모델링의 LDA는 비지도 학습에 속하고 word2vec도 비지도 학습에 속한다.

2.4 샘플(Sample)과 특성(Feature)

중요 용어에 대해 알아보자. 많은 머신 러닝 문제가 1개 이상의 독립 변수 x를 가지고 종속 변수 y를 예측하는 문제이다. 많은 머신 러닝 모델들, 특히 인공 신경망 모델은 독립 변수, 종속 변수, 가중치, 편향 등을 행렬 연산을 통해 연산하는 경우가 많다. 그래서 행렬을 자주 보게 될 것인데, 독립 변수 x의 행렬을 X라고 했을 때, 독립 변수의 개수가 n개 이고 데이터의 개수가 m인 행렬 X는 다음과 같다.

이때 머신 러닝에서는 하나의 데이터, 하나의 행을 샘플(Sample)이라 부르고, 종속 변수 y를 예측하기 위한 각각의 독립 변수x를 특성(Feature)이라고 부른다.

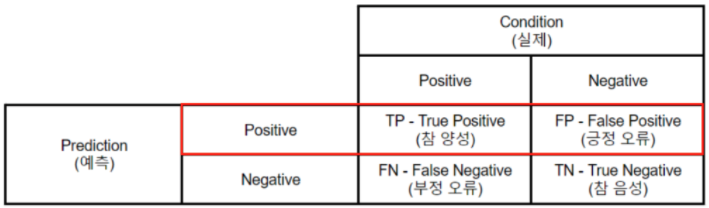
2.5 혼동 행렬(Confusion Matrix)

머신 러닝에서는 맞춘 문제수를 전체 문제수로 나눈 값을 정확도(Accuracy)라고 한다. 하지만 정확도는 맞춘 결과와 틀린 결과에 대한 세부적인 내용을 알려주지는 않는다. 이를 위해 사용하는 것이 혼동 행렬이다.

예를 들어 양성(Positive)과 음성(Negative)을 구분하는 이진 분류가 있다고 했을 때 혼동 행렬은 다음과 같다.

이미지 출처

True 는 정답을 맞춘 경우고, False는 정답을 맞추지 못한 경우다. 그리고 positive와 Negative는 예측된 값들이다. 이를 통해 다음과 같이 알 수 있다. FP는 양성이라 예측했는데, 실제론 음성인 경우이고, FN은 음성이라 예측했는데 실제론 양성인 경우이다.

이 개념을 사용하면 또 새로운 개념인 정밀도(Precision)과 재현율(Recall)이 된다.

1️⃣ 정밀도(Precision)

정밀도는 양성이라고 대답한 전체 케이스에 대한 TP(예측과 정답이 양성으로 같은 경우) 비율이다. 즉, 정밀도를 수식으로 표현하면 다음과 같다.

$ 정밀도 = \frac{TP}{TP + FP} $

2️⃣ 재현율(Recall)

재현율은 실제 값이 양성인 데이터의 전체 개수에 대해서 TP(예측과 정답이 양성으로 같은 경우)의 비율이다. 즉, 양성인 데이터 중에서 얼마나 양성인지를 예측(재현)했는지를 나타낸다.

$ 재현율 = \frac{TP}{TP + FN} $

🤔 근데 이것들을 왜 구해서 어디다 쓰는 것인가?

정의되는 문제의 종류에 따라 다르다.

1. 재현율은 실제값이 positive일 때 예측한 값이 positive일 경우가 중요한 상황일 때 사용된다. 즉 잘못 예측해도 negative인 경우가 적은게 나을 때이다. 단적인 예로, 암 판단 분류 예측을 하는 문제에 있어서 실제로 암이 걸렸는데 예측을 암이 걸리지 않았다고 판단하게 되면 수반되는 위험이 매우 커지기 때문이다.
2. 반대로 정밀도는 모델이 예측한 것이 틀려도 Posivite인 경우가 적은게 나을 경우에 사용된다. 예시로 스팸메일 분류를 생각해보자. 만약 분류 모델이 중요한 업무내용을 담고 있는 메일(Negative)을 스팸메일(Positive)이라 분류하게 된다면 전달되지 못하는 위험한 상황이 발생한다.

➕ F1-score

추가로 성능측정 지표로 F1-score 라는 것이 있는데, 이것은 정밀도와 재현율의 조화평균이다. 수식은 다음과 같다.

$F1Score = 2 * \frac{(재현율 * 정밀도)}{(재현율 + 정밀도)}$

주로 다중 클래스를 분류 모델의 성능 측정 지표로 많이 사용되는데, 이 이유는 단순 정확도(Accuracy)를 구할 때에 데이터가 특정 클래스로 쏠려있는 경우일 때 정확도가 높은 수치를 나타내지만 실제론 그렇지 않은 경우가 생기기 때문이다.

위 사진과 같이 수치는 model2가 훨씬 정확하다고 하지만, model2는 B,C,D에서 10개중 1개 밖에 못맞추는 모델이다. 즉, A만 잘맞추는 모델이 된 것이다. 그렇기에 model2가 model1 보다 좋다고 얘기할 순 없는 것이다.

이렇게 데이터가 균등하지 못한 경우 성능측정을 f1-score를 사용한다. 즉, 조화평균은 단순하게 평균을 구하는 것이 아니라, 큰 값이 있다면 패널티를 주어서, 작은값 위주로 평균을 구하게 된다.

2.6 과적합(Overfitting)과 과소 적합(Underfitting)

학생의 입장이 되어 같은 문제지를 과하게 많이 풀어 문제 번호만 봐도 정답을 맞출 수 있게 되었다 가정하자. 그런데 다른 문제지나 시험을 보면 점수가 안 좋다면 그게 의미가 있을까?

머신러닝에서 이러한 경우와 같이 훈련 데이터를 과하게 학습한 경우를 과적합(Overfitting)이라고 한다. 즉 훈련 데이터에 대해 지나친 일반화를 한 상황이다. 그 결과 훈련 데이터에 대해서 오차가 낮지만, 테스트 데이터에 대해서는 오차가 높아지는 상황이 발생한다. 아래의 스팸 필터 분류기를 예제를 살펴보자.

훈련 횟수가 3~4회를 넘어가게 되면 오차(loss)가 점차 증가하는 양상을 보여준다. 훈련데이터에 대해서는 정확도가 높지만, 테스트 데이터는 정확도가 점차 낮아진다고 볼 수 있다.

그래서 과적합을 방지하기 위해 테스트 데이터에 대한 loss값이 크게 높아지기 전에 훈련을 멈추는 것이 바람직 하지만, 반대로 테스트 데이터의 성능이 올라갈 여지가 있음에도 훈련을 덜 한 상태가 있을 수 있다. 이러한 경우를 과소적합(Underfitting)이라 한다. 훈련자체가 부족한 상태이므로 훈련데이터에 대해서도 보통 정확도가 낮다는 특징이 있다.

딥 러닝을 할 때는 과적합을 막을 수 있는 드롭 아웃(Drop out), 조기 종료(Early Stopping)과 같은 몇 가지 방법이 존재한다.
그 전까지 차근차근 공부해 나가자~!

reference

• k-폴드 교차검증(k-fold cross Validation) : https://nonmeyet.tistory.com/entry/KFold-Cross-Validation%EA%B5%90%EC%B0%A8%EA%B2%80%EC%A6%9D-%EC%A0%95%EC%9D%98-%EB%B0%8F-%EC%84%A4%EB%AA%85
• 정밀도와 재현율 : https://techblog-history-younghunjo1.tistory.com/101
• f1-score : https://nittaku.tistory.com/295

개요

딥 러닝을 이용한 자연어 처리 입문

기계 학습 및 자연어 처리 분야에서 토픽이라는 문서 집합의 추상적인 주제를 발견하기 위한 통계적 모델 중 하나로, 텍스트 본문의 숨겨진 의미 구조를 발견하기 위해 사용되는 텍스트 마이닝 기법인 topic modeling에 대해 알아보자.

1. 잠재 의미 분석(Latent Semantic Analysis, LSA)

LSA는 정확히 토픽 모델링을 위해 최적화 된 알고리즘은 아니지만, 토픽 모델링이라는 분야에 아이디어를 제공한 알고리즘이라 볼 수 있다. 이에 토픽 모델링 알고리즘인 LDA(LSA의 단점 개선한 알고리즘. 이후에 설명)에 앞서 배워보도록 하자.

BoW에 기반한 것들은 단어의 의미를 고려하지 못한다는 단점이 있다. 이를 위한 대안으로 잠재 의미 분석(LSA)이란 방법이 있다. 이 방법을 이해하기 위해서는 선형대수학의 특이값 분해(Singular Value Decomposition, SVD)를 이해할 필요가 있다.

1.1 특이값 분해(Singular Value Decomposition, SVD)

시작하기 앞서, 여기서의 특이값 분해(Singular Value Decomposition, SVD)는 실수 벡터 공간에 한정하여 내용을 설명함을 명시한다. SVD란 A가 m × n 행렬일 때, 다음과 같이 3개의 행렬의 곱으로 분해(decomposition)하는 것을 말한다

그림에서 $V^*$는 위키피디아에서 V의 켤레전치라 표현한다. 여기서 $V^T$와 같다고 보면된다.

$A = U\Sigma V^T$

여기서 각 3개의 행렬은 다음과 같은 조건을 만족한다.

• $U : m \times m $ 직교행렬(orthogonal matrix) ($AA^T = U(\Sigma\Sigma^T)U^T$)
• $V : n \times n $ 직교행렬(orthogonal matrix) ($A^TA = V(\Sigma\Sigma^T)V^T$)
• $\Sigma : m \times n $ 직사각 대각 행렬(diagonal matrix)

➕ 용어 정리

1. 전치 행렬(Transposed Matrix)
   원래 행렬에서 행과 열을 바꾼행렬. 기호는 기존 행렬 표현 우측 위에 T를 붙인다.
   $$ M = \begin{bmatrix}1 & 2 \\ 3 & 4 \\ 5 & 6 \\ \end{bmatrix} M^T = \begin{bmatrix}1 & 3 & 5 \\ 2 & 4 & 6 \\ \end{bmatrix} $$
2. 단위 행렬(Identity Matrix)
   주 대각선의 요소만 1이고 나머진 0인 정사각 행렬. 어떤 행렬에 곱하든 자기 자신이 나옴 ex) $A \times I=A$
   $$ I = \begin{bmatrix}1 & 0 \\ 0 & 1 \\ \end{bmatrix} I = \begin{bmatrix}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{bmatrix} $$
3. 역행렬(Inverse Matrix)
   행렬 A와 어떤 행렬을 곱했을 때 단위 행렬이 나온다면, 이때의 어떤 행렬을 $A$의 역행렬 $A^{-1}$ 이라 표현한다.
   $A \times A^{-1} = I$
   $$ \begin{bmatrix}1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \\ \end{bmatrix} \times \begin{bmatrix} \qquad \\ ? \\ \qquad \\ \end{bmatrix} = \begin{bmatrix}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{bmatrix} $$
4. 직교 행렬(Orthogonal Matrix)
   실수 $n \times n$ 행렬 $A$에 대하여 $A \times A^{-1} = I$를 만족하면서 $A^{-1} \times A = I$를 만족하는 행렬$A$를 직교행렬이라 한다. 또한 직교행렬은 역행렬의 정의를 통해 $A^T = A^{-1}$를 만족한다.
5. 대각 행렬(Diagonal Matrix)
   주 대각선의 원소를 제외한 원소가 모두 0인 행렬을 말한다. 주 대각선의 원소가 a라고 한다면 3 x 3 행렬이라면 아래와 같이 표현할 수 있다.
   $$\Sigma = \begin{bmatrix}a & 0 & 0 \\ 0 & a & 0 \\ 0 & 0 & a \\ \end{bmatrix}$$
   직사각 행렬이 될 경우 잘 보아야 헷갈리지 않는다. m x n 행렬일 때 m > n인 경우(행이 열보다 클 때)이다
   $$\Sigma = \begin{bmatrix}a & 0 & 0 \\ 0 & a & 0 \\ 0 & 0 & a \\ 0 & 0 & 0 \\ \end{bmatrix}$$
   m < n인 경우(열이 행보다 클 때)이다
   $$\Sigma = \begin{bmatrix}a & 0 & 0 & 0 \\ 0 & a & 0 & 0 \\ 0 & 0 & a & 0 \\ \end{bmatrix}$$
   SVD를 통해 나온 대각 행렬은 추가적인 성질을 가지는데, 주 대각원소를 행렬 A의 특이값(singular value)라고 하며, 이를 $\sigma_1, \sigma_2 , ... ,\sigma_r$ 이라 표현한다면 특이값 $\sigma_1, \sigma_2 , ... ,\sigma_r$은 내림차순으로 정렬되어 있다는 특징을 가진다. 즉 다음 행의 값은 그 전 행의 값보다 클 수 없다는 것이다.
   $$\Sigma = \begin{bmatrix}12.4 & 0 & 0 \\ 0 & 9.5 & 0 \\ 0 & 0 & 1.3 \\ \end{bmatrix}$$

간단하게 정리하자면 하나의 행렬 ex) A를 3가지 행렬 $U\Sigma V^T$으로 분해할 수 있고, 그렇게 얻은 대각 행렬 $\Sigma$의 원소들은 A 행렬의 특이값들이 된다는 것 같다.

수학적으로 더욱 자세히 알고 싶다면 https://angeloyeo.github.io/2019/08/01/SVD.html 이런 곳을 참고해보는 건 어떨까.

1.2 절단된 SVD (Truncated SVD)

위에서 설명한 SVD를 full SVD라고 한다. 하지만 LSA의 경우 full SVD에서 나온 3개의 행렬에서 일부 벡터들을 삭제시킨 절단된 SVD(truncated SVD)를 사용하게 된다.

절단을 하면 대각 행렬 $\Sigma$의 원소의 값 중에서 상위값 $t$개만 남게 된다. 절단된 SVD를 수행하면 값의 손실이 일어난다. 왜 절단된 것을 사용하는가? 노이즈에 영향을 받을 수 있기 때문이다. 그래서 $t$를 하이퍼파라미터로 사용한다. 결과적으로 $t$를 크게 잡으면 기존 행렬 A로 부터 다양한 의미를 가져갈 수 있지만, $t$를 작게 잡아야 노이즈를 제거할 수 있다. 게다가 차원이 줄어들어 계산 비용 또한 낮아진다.

1.3 잠재 의미 분석(Latent Semantic Analysis, LSA)

이것을 사용하게된 배경부터 다시 생각해보자. 기존의 DTM이나 TF-IDF행렬은 단어의 의미를 전혀 고려하지 못한다는 단점을 갖고 있었다. LSA는 기본적으로 DTM이나, TF-IDF 행렬에 절단된 SVD(truncated SVD)를 사용하여 차원을 축소시키고, 단어들의 잠재적인 의미를 끌어낸다는 아이디어를 갖고 있다.

그래서 어떻게 코드로 구현될까. 어서 실습해보자. 아, numpy와 함께. (pip install numpy 필수!)

import numpy as np
A=np.array([[0,0,0,1,0,1,1,0,0],
            [0,0,0,1,1,0,1,0,0],
            [0,1,1,0,2,0,0,0,0],
            [1,0,0,0,0,0,0,1,1]])
np.shape(A) # (4, 9)

DTM 행렬 A를 예를 들어보겠다. shape을 통해 4 x 9 인 행렬임을 알 수 있다. 이 행렬을 full SVD를 수행해보자.

U, s, VT = np.linalg.svd(A, full_matrices = True)

대각행렬 $\Sigma$ 를 s라고 하고, $V^T$ 를 VT라 한다면 코드 한줄로 SVD를 수행할 수 있다.
특이한 점은 numpy의 linalg.svd()는 분해 결과로 대각 행렬이 아니라, 특이값의 리스트로 반환한다. 게다가 내림차순을 보이는 것을 확인할 수 있다.

print(s.round(2)) # [2.69 2.05 1.73 0.77]
np.shape(s) # (4, )
# 행렬로 바꿔주기
S = np.zeros((4, 9)) # 대각 행렬의 크기인 4 x 9의 임의의 행렬 생성
S[:4, :4] = np.diag(s) # 특이값을 대각행렬에 삽입
print(S.round(2))
np.shape(S) # (4,9)

이제 t를 2로 한 SVD를 해보자. 위에서 구한 값에서 행과 열을 맞춰줌으로 제거할 수 있다.

S=S[:2,:2]
U=U[:,:2]
VT=VT[:2,:]

이렇게 자른 행렬을 다시 붙여서 $A'$ 행렬을 만들어 원래 행렬 $A$와 비교해보자.

A_prime=np.dot(np.dot(U,S), VT)
print(A)
print(A_prime.round(2))

[[0 0 0 1 0 1 1 0 0]
 [0 0 0 1 1 0 1 0 0]
 [0 1 1 0 2 0 0 0 0]
 [1 0 0 0 0 0 0 1 1]]
[[ 0.   -0.17 -0.17  1.08  0.12  0.62  1.08 -0.   -0.  ]
 [ 0.    0.2   0.2   0.91  0.86  0.45  0.91  0.    0.  ]
 [ 0.    0.93  0.93  0.03  2.05 -0.17  0.03  0.    0.  ]
 [ 0.    0.    0.    0.    0.    0.    0.    0.    0.  ]]

대체적으로 기존에 0인 값들은 0에 가까운 값이 나오고, 1인 값들은 1에 가까운 값이 나오는 것을 볼 수 있다. 또한 값이 제대로 복구되지 않은 구간도 존재하는 것 같다. 이것들이 대체 무슨 의미를 가지고 있을까?

• 축소된 U는 (4 x 2)의 크기를 가지는데, 이는 (문서의 개수 x 토픽의 수 t) 의 크기라고 할 수 있다. 4개의 문서 각각을 2개의 값으로 표현한다. 즉, U의 각 행은 잠재 의미를 표현하기 위한 수치화 된 각각의 문서 벡터라고 볼 수 있다.
• 같은 맥락으로 축소된 VT는 토픽의 수와 단어의 개수 트기이다. 각 열은 잠재의미를 표현하기 위해 수치화된 각각의 단어 벡터라고 볼 수 있다.

➕ 내가 받아 드린 바로는, DTM을 기준으로 설명하자면,

1. 하나로된 단어와 문서행렬($A$= d(문서수) x w(단어수) 행렬)을
2. 특이값으로 분해($A= U \Sigma V^T$)하여 토픽으로 차원을 줄이면($\Sigma $= t x t 행렬로 줄임)
3. 문서와 토픽간의 행렬($U \times \Sigma = U_t$= d x t) / 토픽과 단어간의 행렬($\Sigma \times V^T = V^T_t$= t x w)로 만듬
4. 이렇게 나온 $U_t$, $V^T_t$ 행렬을 이용해서 각 문서(또는 단어) 사이의 코사인 유사도와 같이 유사도를 구할 수 있다.

이렇게 결과로 나온 문서 벡터와 단어 벡터를 통해 다른 문서의 유사도, 다른 단어의 유사도, 단어(쿼리)로부터 문서의 유사도를 구하는 것들이 가능해진다.

이 영상을 보면 이해하는데 도움이 될까 싶어서 링크를 달아둔다. https://www.youtube.com/watch?v=GVPTGq53H5I

scikit-learn 을 이용하여 tf-idf나 dtm 행렬을 인풋 (ex. 밑에 코드에선 X)으로 truncated SVD를 쉽게 구해볼 수 있다.

from sklearn.decomposition import TruncatedSVD
svd_model = TruncatedSVD(n_components=20, algorithm='randomized', n_iter=100, random_state=122)
svd_model.fit(X)
len(svd_model.components_)

n_components는 토픽의 수(이전 설명의 t)이고, svd_model.components_는 VT 행렬에 해당한다.
이렇게 추출된 행렬을 사용하여 예를 들어 특정 토픽에 가장 큰 값을 가지는 단어를 찾아낼 수 있다.
토픽에 행이므로 한 행의 요소들 중에 제일 높은 값을 가지는 인덱스를 찾으면 단어를 알 수 있다.

1.4 LSA의 장단점

LSA는 쉽고 빠르게 구현이 가능할 뿐만 아니라 단어의 잠재적인 의미를 이끌어낼 수 있어 문서의 유사도 계산등에서 좋은 성능을 보여준다는 장점을 갖고 있다. 하지만 SVD의 특성상 새로운 정보에 대해 업데이트가 어렵다. 처음부터 다시 계산해야 하기 때문이다.

2. 잠재 디리클레 할당(Latent Dirichlet Allocation, LDA)

토픽 모델링은 문서의 집합에서 토픽을 찾아내는 프로세스를 말한다. 문서들은 토픽들의 혼합으로 구성되어져 있으며, 토픽들은 확률 분포에 기반하여 단어들을 생성한다고 가정한다. 데이터가 주어지면 LDA는 문서가 생성되던 과정을 역추척한다. 이게 무슨 말일까?

2.1 개요

우선 내부 메커니즘을 이해하기 전 LDA를 일종의 블랙 박스로 보고 LDA에 문서 집합을 입력하면, 어떤 결과를 보여주는지 다음 예를 보고 확인해보자.

문서1 : 저는 사과랑 바나나를 먹어요
문서2 : 우리는 귀여운 강아지가 좋아요
문서3 : 저의 깜찍하고 귀여운 강아지가 바나나를 먹어요

위와 같에 3개의 문서가 있다고 하자. LDA를 수행할 때 문서 집합에서 토픽이 몇 개가 존재할지 가정하는 것은 사용자가 해야 할 일이다. 여기서는 LDA에 2개의 토픽을 찾으라고 가정하자.

# 각 문서의 토픽 분포
문서1 : 토픽 A 100%
문서2 : 토픽 B 100%
문서3 : 토픽 B 60%, 토픽 A 40%

# 각 토픽의 단어 분포
토픽A : 사과 20%, 바나나 40%, 먹어요 40%, 귀여운 0%, 강아지 0%, 깜찍하고 0%, 좋아요 0%
토픽B : 사과 0%, 바나나 0%, 먹어요 0%, 귀여운 33%, 강아지 33%, 깜찍하고 16%, 좋아요 16%

LDA는 토픽의 제목을 정해주지 않지만, 이 시점에서 알고리즘의 사용자는 위 결과로부터 두 토픽이 각각 과일에 대한/강아지에 대한 토픽이라고 판단해볼 수 있다. 이거까지만 봐서는 솔직히 LSA와 LDA의 차이를 잘 모르겠다.

2.2 LDA의 가정

LDA는 문서의 집합으로부터 어떤 토픽이 존재하는지를 알아내기 위한 알고리즘이다. 앞서 배운 빈도수 기반의 표현 방법인 BoW의 행렬 DTM 또는 TF-IDF 행렬을 입력으로 하는데, 이로부터 알 수 있는 사실은 단어의 순서는 신경쓰지 않겠다는 점이다. 그리고 문서들로부터 토픽을 뽑아내기 위해 모든 문서 하나하나가 작성될 때 그 문서의 작성자는 이러한 생각을 했다. '나는 이 문서를 작성하기 위해서 이런 주제들을 넣을거고, 이런 주제들을 위해 이런 단어를 넣을 거야.' 아직 뭔소린지 모르겠다. 구체적으로 살펴보자.

1. 문서에 사용할 단어의 개수 N을 정한다. ex) 5개 단어 정한다.

2. 문서에 사용할 토픽의 혼합을 확률 분포에 기반하여 결정한다.

   • 위 예제 같이 토픽이 2개라고 했을 때, 강아지 토픽을 60%, 과일 토픽을 40%와 같이 선택할 수 있다.

3. 문서에 사용할 각 단어를 (아래와 같이) 정합니다.

   1. 토픽 분포에서 토픽 T를 확률적으로 고른다.
   • ex) 60% 확률로 강아지 토픽을 선택하고, 40% 확률로 과일 토픽을 선택할 수 있다.
   2. 선택한 토픽 T에서 단어의 출현 확률 분포에 기반해 문서에 사용할 단어를 고른다.
   • ex) 강아지 토픽을 선택하였다면, 33% 확률로 강아지란 단어를 선택할 수 있다. 이제 3을 반복하면서 문서 완성.

이러한 과정을 통해 문서가 작성되었다는 가정 하에 LDA는 토픽을 뽑아내기 위하여 위 과정을 역으로 추적하는 역공학(reverse engineering)을 수행한다. 솔직히 아직도 모르겠다.

2.3 LDA 수행

위에서 나온 수행과정을 구체적으로 정리해보자.

1️⃣ 사용자는 알고리즘에게 토픽의 개수 k를 알려준다.

토픽의 개수를 알려주는 것은 사용자의 역할이다. LDA는 토픽의 개수 k를 입력받으면, k개의 토픽이 M개의 전체 문서에 걸쳐 분포되어 있다고 가정한다.

2️⃣ 모든 단어를 k개 중 하나의 토픽에 할당한다.

이제 LDA는 모든 문서의 모든 단어에 대해서 k개 중 하나의 토픽을 랜덤으로 할당한다. 이 작업이 끝나면 각 문서는 토픽을 가지며, 토픽은 단어 분포를 가지는 상태이다. 랜덤으로 할당했기에, 전부 틀린 상태다. 만약 한 단어가 한 문서에 2회 이상 등장했다면 각 단어는 서로 다른 토픽에 할당되었을 수도 있다.

3️⃣ 이제 모든 문서의 모든 단어에 대해 아래 사항을 반복한다.

1. 어떤 문서의 각 단어 w는 자신은 잘못된 토픽에 할당되어져 있지만, 다른 단어들은 전부 올바른 토픽에 할당되어졌다고 가정하자. 이에 따라 단어 w는 아래 두가지 기준에 따라 토픽이 재할당된다.
   • p(topic t | document d) : 문서 d의 단어들 중 토픽 t에 해당하는 단어들의 비율
   • p(word w | topic t) : 각 토픽들 t에서 해당 단어 w의 분포

간단한 예제로 이해해보자.

여기서 빨간색으로 칠한 사과의 토픽을 결정하려고 한다.

두번째 방법은 모든 문서에서 등장한 같은 단어의 토픽 분포를 보고 결정한다. 여기서도 다른 사과가 A인 경우가 많아서 A 로 할당할 확률이 높다고 볼 수 있다.

여기서 드는 의문점은 처음에 LDA가 각 문서들에 토픽을 할당할 때는 어떤 기준으로 진행하는지 궁금했는데, 이곳에서 본 바 처음엔 랜덤하게 할당한다고 한다. 이후 위에서 설명한 과정을 iteration을 돌면서 수정해나가는 것으로 이해했다. 자세히 알고싶다면 저 링크를 들어가보는 것을 추천한다. 난 아무것도 몰러유...😵‍💫

2.4 LSA 와 LDA의 차이점

• LSA : DTM을 차원 축소 하여 축소 차원에서 근접 단어들을 토픽으로 묶는다.
• LDA : 단어가 특정 토픽에 존재할 확률과 문서에 특정 토픽이 존재할 확률을 결합확률로 추정하여 토픽을 추출한다.

결국 LSA나, LDA는 단어의 순서를 고려하지 않으므로 단어들의 빈도수만을 가지고 표현한다.

reference

• 특이값 분해(SVD)
  • https://ko.wikipedia.org/wiki/%ED%8A%B9%EC%9E%87%EA%B0%92_%EB%B6%84%ED%95%B4
  • https://angeloyeo.github.io/2019/08/01/SVD.html
• 잠재 디클렐레 분석(LDA)
  • https://ratsgo.github.io/from%20frequency%20to%20semantics/2017/06/01/LDA/

개요

딥러닝을 이용한 자연어 처리 입문
기계가 문서의 유사도를 구할때 문서들 간에 동일한 단어 또는 비슷한 단어가 얼마나 공통적으로 많이 사용되었는지에 의존한다. 그렇기에 유사도의 성능은 단어들을 어떤 방법으로 수치화하여 표현했는지(DTM, Word2Vec 등), 문서 간의 단어들의 차이를 어떤 방법으로 계산(유클리드 거리, 코사인 유사도 등)했는지에 따라 다르다.

1. 코사인 유사도(Cosine Similarity)

단어를 수치화할 수 있다면 수치를 통해 계산을 할 수 있다. 유사도를 구하는 계산법에 대해 알아보자.

1.1 코사인 유사도란?

두 벡터 간의 코사인 각도를 이용하여 구할 수 있는 두 벡터의 유사도를 의미한다. 두 벡터의 방향이 완전히 동일한 경우에는 1의 값을 가지고, 90도의 각을 이루면 0의 값, 180도로 반대의 방향을 가지면 -1의 값을 가지게 된다. 즉, -1 이상 1이하의 값을 가지며 값이 1에 가까울수록 유사도가 높다고 판단할 수 있다. 직관적으로 이해하자면 두 벡터가 가르키는 방향이 얼마나 유사한지를 의미한다.

식으로 표현하면 다음과 같다.
$similarity = \cos (\Theta) = \frac{A \cdot B}{\parallel A \parallel \parallel B \parallel} = \frac{\sum_{i=1}^n A_i \times B_i}{\sqrt{\sum_{i=1}^n(A_i)^2} \times \sqrt{\sum_{i=1}^n(B_i)^2}}$

방향이 얼마나 유사한지를 판단하는 것을 두 벡터 사이의 각도를 구하는 것으로 접근했다. 왼쪽 그림은 두 벡터 a, b의 스칼라곱($A \cdot B$)을 표현한 그림이다. $\theta$ 값이 작아진다면 같은 방향을 향한다고 볼 수 있지 않는가? 오른쪽 그림을 통해 $\theta$값이 작아지면 자연스럽게 $\cos{\theta}$ 의 값이 1에 가까워 짐을 알 수 있다.(파란 점선이 코사인 함수. 각도가 0일 때 1임을 알 수 있다.) 그래서 처음 설명에서 1에 가까울 수록 두 벡터 간의 각도가 0에 가까우니 같은 방향을 향하므로 유사도가 높다고 말할 수 있는 것이다.

그리고 왜 뚱딴지 같이 스칼라곱이 나왔나 싶을 수 있다. 스칼라곱 공식 살펴보자.
$ A \cdot B = \cos{\theta} \parallel A \parallel \parallel B \parallel $
사실 스칼라곱 공식에서 $ \parallel A \parallel \parallel B \parallel $을 이항시킴으로 $\cos{\theta}$를 구하는 공식이 유도 됨을 알 수 있다.

➕ $\parallel A \parallel$ 이것은 norm 이라고 하는데 구글에 검색하면 더욱 자세히 알 수 있다.

그래도 감이 안 올땐 역시 코드를 보자. 코드로 보면(numpy를 이용하여) 쉽게 구현할 수 있다.

from numpy import dot
from numpy.linalg import norm
import numpy as np
def cos_sim(A, B):
       return dot(A, B)/(norm(A)*norm(B))

이것을 이용해 보기 위해 간단한 예를 들어 다음과 같은 백터가 있다고 생각해보자.

doc1=np.array([0,1,1,1])
doc2=np.array([1,0,1,1])
doc3=np.array([2,0,2,2])

각각의 문서 벡터들의 유사도를 구해본다면

print(cos_sim(doc1, doc2)) #문서1과 문서2의 코사인 유사도
print(cos_sim(doc1, doc3)) #문서1과 문서3의 코사인 유사도
print(cos_sim(doc2, doc3)) #문서2과 문서3의 코사인 유사도

0.67
0.67
1.00

결과는 위와 같다. 신기한 것은 문서1과 문서2의 코사인 유사도와 문서1과 문서3의 코사인 유사도가 같다는 것이다. 코사인 유사도는 특정 문서의 단어 빈도수가 일정하게 더 높아질 때 다른 문서보다 유사도가 높게 나오는 것을 방지할 수 있다. 즉, 코사인 유사도는 크기보다 방향으로 유사도를 따지기에 앞서 말한 동일한 패턴으로의 크기가 증가하는 경우와 같을 때 공정한 비교를 할 수 있도록 도와준다.

2. 여러가지 유사도 기법

코사인 유사도 외의 여러가지 유사도 기법에 대해 알아보자.

2.1 유클리드 거리(Euclidean distance)

유클리드 거리는 문서 유사도를 구할 때 자카드 유사도나 코사인 유사도만큼 유용한 방법은 아니다. 하지만 여러 가지 방법을 이해하고, 시도해보는 것 자체만으로 다른 개념들을 이해할 때 도움이 되므로 의미가 있다.

다차원 공간에서 두개의 점 p와 q가 각각 $p = (p_1,p_2,p_3,...,p_n)$ 과 $q = (q_1,q_2,q_3,...,q_n)$ 의 좌표를 가질 때 두 점 사이의 거리를 계산하는 유클리드 거리 공식은 다음과 같다.

$\sqrt{(q_1-p_1)^2 + (q_2-p_2)^2 + ... + (q_n-p_n)^2} = \sqrt{\sum_{i=1}^n(q_i-p_i)^2}$

다차원 공간이라 복잡해 보이지만, 2차원 공간이라 가정한다면 피타고라스의 정리라고 생각하면 된다.
numpy를 이용해 docQ와 가장 유사한(가까운) 문서를 찾는 간단한 예제를 구현해보자.

import numpy as np
def dist(x,y):   
    return np.sqrt(np.sum((x-y)**2))

doc1 = np.array((2,3,0,1))
doc2 = np.array((1,2,3,1))
doc3 = np.array((2,1,2,2))
docQ = np.array((1,1,0,1))

print(dist(doc1,docQ)) # 2.23606797749979
print(dist(doc2,docQ)) # 3.1622776601683795
print(dist(doc3,docQ)) # 2.449489742783178

문서 1이 제일 가까우므로 유사하다고 볼 수 있다.

2.2 자카드 유사도(Jaccard similarity)

A와 B 두개의 집합이 있다고 하자. 합집합에서 교집합의 비율을 구한다면 두 집합 A와 B의 유사도를 구할 수 있지 않을까?라는 아이디어가 바로 자카드 유사도의 아이디어이다. 자카드 유사도는 0과 1사이의 값을 가지게 되는데, 동일하면 1의 값을 가지고 공통원소가 없다면 0의 값을 가진다.

J를 자카드 유사도 함수라고 하였을 때, 수식으로 표현하면 다음과 같다.
$J(A,B) = \frac{|A \cap B|}{|A \cup B|} = \frac{|A \cap B|}{|A|+|B|-||A \cap B||}$

코드로는 set을 이용한다면 간단히 구현할 수 있다.

doc1 = "apple banana everyone like likey watch card holder"
doc2 = "apple banana coupon passport love you"

# 토큰화를 수행합니다.
tokenized_doc1 = doc1.split()
tokenized_doc2 = doc2.split()

문서 별 토큰화 결과를 set으로 만들어 합집합과 교집합을 구하여 계산한다.

union = set(tokenized_doc1).union(set(tokenized_doc2))
print(union) 

{'card', 'holder', 'passport', 'banana', 'apple', 'love', 'you', 'likey', 'coupon', 'like', 'watch', 'everyone'}

intersection = set(tokenized_doc1).intersection(set(tokenized_doc2))
print(intersection) # {'banana', 'apple'}

print(len(intersection)/len(union)) # 0.166666666

이렇게 구한 값은 자카드 유사도이자, 두 문서에서의 총 단어 집합 중 공통적으로 등장한 단어의 비율이라고도 할 수 있다.

2.3 레벤슈타인 거리(Levenshtein distance)

• 레벤슈타인 거리는 편집 거리라고도 하는데, 두 문자열이 얼마나 다른지를 나타내는 거리 중 하나이다
• 문자를 삽입, 삭제, 치환하여 다른 문자열로 변형하는데 필요한 최소 횟수를 구하여, 이것을 점수로 나타낼 수 있다.
• 철자검사기 등에서 두 문자열이 어느 정도 유사한지 값으로 나타내는 방법의 하나
• 1965년 러시아의 브라디미르 레벤슈타인이 고안함

2.4 n-gram을 이용한 유사도

이전포스팅 [자연어처리 입문] 2. 언어 모델 에서 다뤘던 부분이라 구체적인 부분은 참고 바란다.
이 n-gram을 이용하여 두 문장이 같은 문자를 사용하지만 순서가 바뀌거나 오타교정 등에 많이 사용될 수 있을 것 같다.

reference

• 스칼라곱 : https://ko.wikipedia.org/wiki/%EC%8A%A4%EC%B9%BC%EB%9D%BC%EA%B3%B1
• 삼각함수 : https://ko.wikipedia.org/wiki/%EC%82%BC%EA%B0%81%ED%95%A8%EC%88%98
• 레벤슈타인 : https://zetawiki.com/wiki/%EB%A0%88%EB%B2%A4%EC%8A%88%ED%83%80%EC%9D%B8_%EA%B1%B0%EB%A6%AC

개요

딥 러닝을 이용한 자연어 처리 입문
자연어처리를 위해서는 문자를 숫자로 수치화할 필요가 있다. 첫 발자국인 카운트 기반의 단어표현에 대해 알아보려고 한다.

1. 다양한 단어의 표현 방법

시작하기에 앞서 카운트 기반의 단어 표현 방법 외에도 다양한 단어의 표현 방법에는 어떤 것이 있는지 간략하게 보고 가겠다.

1.1 단어의 표현 방법

크게 국소 표현(Local Representation) 방법(또는 이산 표현)과 분산 표현(Distributed Representation) 방법(또는 연속 표현)으로 나뉜다.

1. 국소 표현(Local Representation) 또는 이산 표현(Discrete Representation)
   • 특징 : 해당 단어 그 자체만 보고, 특정값을 매핑하여 단어를 표현하는 방법
     ex) 강아지, 고양이, 친칠라 라는 단어가 있을 때 각 단어에 1번, 2번, 3번 등과 같은 숫자를 맵핑(mapping)하여 부여한다.
   • 종류 : One-Hot Vector, N-gram, count base(Bag of Words) 등
2. 분산 표현(Distributed Representation) 또는 연속 표현(Continuous Representation)
   • 특징 : 그 단어를 표현하고자 주변을 참고하여 단어를 표현하는 방법
     ex) 강아지라는 단어 근처에 주로 귀여운, 사랑스러운이라는 단어가 자주 등장하므로, 강아지라는 단어는 귀엽운, 사랑스러운 느낌이다라고 단어를 정의한다.
   • 종류 : prediction base(Word2Vec, FastText), count base(LSA, Glove) 등

즉, 국소 표현 방법에서 단어의 의미, 느낌을 표현할 수 없지만, 분산 표현 방법은 단어의 느낌을 표현할 수 있다는 차이가 있다.

2. Bag of Words(Bow)

2.1 Bag of Words 란

Bag of Words란 단어들의 순서는 전혀 고려하지 않고, 단어들의 출현 빈도(frequency)에만 집중하는 텍스트 데이터의 수치화 표현 방법이다. 만드는 과정은 다음과 같다.

1. 우선, 각 단어에 고유한 정수 인덱스를 부여한다.
2. 각 인덱스의 위치에 단어 토큰의 등장 회수를 기독한 벡터를 만든다.

1번은 뭐 그렇다 치는데 2번은 살짝 무슨 소린지 느낌이 잘 안온다. 다음 예시를 통해 이해해보자.

from konlpy.tag import Okt
okt=Okt()  

token="내꺼인듯 내꺼아닌 내꺼같은 너란 사람은 참"
token=okt.morphs(token) # 형태소분석
word2index={}  # 단어에 인덱스 부여
bow=[]    # 빈도수저장


# 토큰하나씩 들고온다
for voca in token:
    # word2index 안에 해당 토큰이 없다면
    if voca not in word2index:  
        # 인덱스(word2index길이만큼)를 지정해주고
        word2index[voca]=len(word2index)
        # 단어가 등장했으니, 빈도수를 담는 리스트에 1을 넣어준다.
        bow.insert(len(word2index)-1,1)
    # word2index 안에 있는 토큰이라면
    else:
        # 해당 토큰의 인덱스를 가져와서
        index=word2index[voca]
        # 한 번 더나왔으니 그 토큰의 인덱스로 빈도수 리스트에 접근하여 값을 1을 더해준다
        bow[index]=bow[index]+1

결과

print(word2index)
# {'내꺼인듯': 0, '내꺼': 1, '아닌': 2, '같은': 3, '너': 4, '란': 5, '사람': 6, '은': 7, '참': 8}
print(bow)
# [1, 2, 1, 1, 1, 1, 1, 1, 1]

내꺼라는 단어가 두번 나와서 2라고 적혔고, 나머지는 1번 나와서 위와 같은 결과가 나왔다.

즉, 각 token(중복없이)에 인덱스를 부여하고, 해당 token의 빈도수를 기록한 것을 bag에 담아놓는다. 이렇게 bow화된 bag을 이용하여 이후에 어떤 문장이 주어지면, 그 문장을 token화 한 뒤, bag에서 해당 token의 빈도수를 가져와 위 예시의 bow와 같이 단어를 정수화 된 리스트로 만들 수 있다.

2.2 CountVectorizer 클래스로 BoW 만들기

사이킷 런(scikit-learn)에서 단어의 빈도를 Count 하여 Vector로 만드는 CountVectorizer 클래스를 지원한다.

from sklearn.feature_extraction.text import CountVectorizer
corpus = ['내꺼인듯 내꺼아닌 내꺼같은 너란 사람은 참','아니 왜 한 글 자 는 없 어 지 는 거 지']
vector = CountVectorizer()

print(vector.fit_transform(corpus).toarray()) # 코퍼스로부터 각 단어의 빈도 수를 기록한다.
print(vector.vocabulary_) # 각 단어의 인덱스가 어떻게 부여되었는지를 보여준다. 

print 결과

[[1 1 1 1 1 0]
 [0 0 0 0 0 1]]
{'내꺼인듯': 2, '내꺼아닌': 1, '내꺼같은': 0, '너란': 3, '사람은': 4, '아니': 5}

2.1 에서 했던 과정을 아주 손쉽게 진행할 수 있다. 하지만 결과에서 보면 내부 로직에 의해 한글자 이하는 포함시키지 않고, 띄어쓰기로 구분하여 하기 때문에 토큰화하기 때문에, 띄어쓰기를 구분자로 한 토큰화된 결과를 인풋으로 넣거나(ex. 내꺼인듯 내꺼 아닌 내꺼 같은 너란 ...), 한국어에 특화된 다른 라이브러리를 이용하면 좋을 것 같다.

2.3 정리

Bow를 사용한다는 것은 그 문서에서 각 단어가 얼마나 자주 등장했는지를 보겠다는 것이다. 그리고 각 단어에 대한 빈도수를 수치화 하겠다는 것은 결국 텍스트 내에서 어떤 단어들이 중요한지를 보고싶다는 의미로 함축된다. 그렇기에 불용어와 같은 별로 의미를 갖지 않는 단어들을 제거해줘야 더 의미있는 단어들만 사용하여 정확도를 올릴 수 있다. 하지만 count 기반이다 보니 중요한 것은 빈도수가 낮거나, bag안에 없는 단어들은 그만큼 의미를 두지 않는다는 점이다. 이후 DTM의 한계에서 더 자세히 알아 보도록하자.

3. 문서 단어 행렬(Document-Term Matrix, DTM)

각 문서에 대한 BoW 표현 방법을 그대로 갖고와서, 서로 다른 문서들의 BoW들을 결합한 표현 방법이다. 이하 DTM이라 명명, 행과 열을 반대로하면 TDM이라 부르기도 함. 이 방법을 통해 서로 다른 문서들을 비교할 수 있게 된다.

3.1 문서 단어 행렬 (DTM)의 표기법

문서 단어 행렬(DTM)이란 다수의 문서에서 등장하는 각 단어들의 빈도를 행렬로 표현한 것을 말한다. 쉽게 생각하면 각 문서에 대한 BoW를 하나의 행렬로 만든 것으로 생각할 수 있다.

문서1 : 먹고 싶은 사과
문서2 : 먹고 싶은 바나나
문서3 : 길고 노란 바나나 바나나
문서4 : 저는 과일이 좋아요

이를 문서 단어 행렬로 표현하면 다음과 같다.

이처럼 각 문서에서 등장한 단어의 빈도를 행렬의 값으로 표기하여 서로 비교할 수 있도록 수치화 할 수 있다.

3.2 문서 단어 행렬(DTM)의 한계

매우 간단하고 구현하기도 쉽지만, 본질적으로 가지는 몇 가지 한계들이 있다.

3.2.1 희소표현(Sparse representation)

원-핫 백터는 단어 집합의 크기가 벡터의 차원이 되고 대부분의 값이 0이 된다는 특징이 있다. 이 특징은 공간적 낭비와 계산 리소스를 증가시킬 수 있다는 점에서 원-핫 벡터의 단점이었다. DTM도 마찬가지다. 각 행을 문서 벡터라고 한다면, 각 문서 벡터의 차원은 원-핫 벡터와 마찬가지로 전체 단어 집합의 크기를 가진다. 만약 corpus가 방대하다면 문서 벡터의 차원은 수백만의 차원을 가질 수도 있다. 또한 대부분의 값이 0을 가질 수도 있다.

원-핫 벡터나 DTM과 같은 대부분의 값이 0인 표현을 희소 벡터(Sparse vector) 또는 희소 행렬(Sparse matrix)라고 부른다. 희소 벡터는 많은 양의 저장 공간과 계산을 위한 리소스를 필요하기 때문에, 전처리를 통해 단어 집합의 크기를 줄이는 일은 BoW 표현을 사용하는 모델에서 중요할 수 있다. 이에 대한 방법으론, 구두점, 빈도수 낮은 단어 / 불용어 제거하고 어간이나 표제어 추출을 통해 단어를 정규화하여 단어 집합의 크기를 줄일 수 있다.

3.2.2 단순 빈도 수 기반 접근

영어에 대해 DTM을 만들었을 때, 불용어인 'the'는 어떤 문서이든 자주 등장할 수 밖에 없다. 그래서 유사한 문서인지 비교할 때, 단순 the가 빈도수가 높다고 유사한 문서라고 판단해선 안 된다. 불용어와 중요 단어에 대해 가중치를 줄 수 있는 방법은 없을까? 그래서 등장한 것이 TF-IDF이다.

4. TF-IDF(Term Frequency-Inverse Document Frequency)

TF-IDF 가중치를 이용하여 기존의 DTM을 사용하는 것보다 더 많은 정보를 고려하여 문서들을 비교할 수 있다. (주의할 점은 TF-IDF가 DTM보다 항상 성능이 뛰어나진 않다)

4.1 TF-IDF(단어 빈도 - 역 문서 빈도)

단어의 빈도와 역 문서 빈도(문서의 빈도에 특정 식을 취함)를 사용하여 DTM 내의 각 단어들마다 중요한 정도를 가중치로 주는 방법이다. 우선 DTM을 만든 후, TF-IDF 가중치를 부여한다. TF-IDF는 TF와 IDF를 곱한 값을 의미한다.

주로 사용되는 경우

1. 문서의 유사도를 구하는 작업
2. 검색 시스템에서 검색 결과의 중요도를 정하는 작업
3. 문서 내에서 특정 단어의 중요도를 구하는 작업

문서를 d, 단어를 t 문서의 총 개수를 n이라고 표현할 때, TF, DF, IDF 각각은 다음과 같이 정의할 수 있다.

1. tf(d,t) : 특정 문서 d에서 특정 단어 t의 등장 횟수.

DTM의 한 행이 하나의 문서에서 나온 단어의 빈도수 벡터이므로 TF는 DTM에서 이미 구했다고 볼 수 있다.

2. df(t) : 특정 단어 t가 등장한 문서의 수

여기서 특정 단어가 각 문서, 또는 문서들에서 몇 번 등장했는지는 관심가지지 않고, 등장한 문서 수만 관심을 가진다. 예를 들어 바나나가 각 문서에서 등장했는지 안했는지만 카운트하지, 하나의 문서에 몇 번 등장했는지까지 고려하지 않는다.

• ex) 문서 1: 바나나 2번 출현, 문서 2: 바나나 1번 출현, 문서 3: 바나나 0번 출현.
  이 경우 바나나는 총 3번 등장했지만, 바나나가 존재한 문서는 2개 뿐이기에 -> df(바나나) = 2

3. idf(d,t) : df(t)에 반비례하는 수

$ idf(d,f) = \log{(\frac{n}{1+df(t)})}$

반비례라면 당연 df의 역수지 않을까 생각했지만, log와 분모에 1을 더하는 것은 왜일까 라는 생각이 든다. 이유는 듣고보면 이해가 된다. log를 사용하지 않으면 분자인 문서수 n이 커질 수록, idf의 값은 기하급수적으로 커지게 때문에 log를 취한다(여기서 로그의 밑은 2나 10이나 상관없지만, 10을 이용한다). 그리고 1을 더하는 것은 df가 0일 경우가 있을 수도 있으니 0으로 나누는 것을 방지 위함이다. 이것을 스무딩(smoothing) 처리라 표현한다.

• ex) 총 문서 10개 중 $n = 10$

1. 문서1에서 '바나나'가 100번 등장했다 가정하고 $tf(문서1,바나나) = 100 $
   모든 문서에 바나나가 있을경우 $df(바나나) = 10$
   idf 값은 -0.04이 된다. $idf = \log{\left(\frac{n}{df(바나나)+1}\right)} = \log{(\frac{10}{11})} = -0.04 $
   문서 1의 '바나나'의 tf-idf 값은 -4 이 된다. $tf(문서1,바나나) \times idf(바나나) = 100 \times -0.04 = -4 $
   => 이와 같이 idf가 음수가 되는 경우 tf-idf 값은 보통 0으로 처리한다.

2. 같은 문서인 문서 1에 '맛있다' 라는 단어가 50번 등장하고 $tf(문서1,맛있다) = 50 $
   문서 1에만 존재한다면 $df(맛있다) = 1$
   idf 값은 0.7이 되므로 $idf(맛있다)=\log{(\frac{10}{2})} = 0.7$
   문서1에서 '맛있다'의 tf- idf 값은 100이 된다 $tf(문서1,맛있다) \times idf(맛있다) = 50 \times 0.7 = 35$

위 예시를 통해 알 수 있는 것은, idf의 경우 모든 문서에서 등장할 경우 값이 0이 되거나 음수가 될 수 있다. 이 경우는 모든 문서에서 등장하므로 가치가 없다고 판단하는 것이다.

4.2 TF-IDF 정리

1. tf 관점 : 문서 내에 빈도수가 높은 단어가 중요하다고 판단.
2. idf 관점 : 해당 단어가 해당 문서에서 외에 다른 문서에 많이 등장하지 않은 경우 중요하다고 판단.
   위 예시에서 '맛있다' 처럼 한 문서에만 존재시 idf값이 커져서 문서 1에서 '맛있다' 라는 단어가 핵심어가 될 수 있음.

결과적으로 idf 값은 해당 단어가 각 문서에 존재한 경우가 적을 수록(df 값이 작을 수록) 분모가 작으므로 값이 커진다. 이것을 tf에 곱해주므로 해당 문서 내의 단어에 가중치를 줄 수 있다.

➕ scikit-learn 사용시 tf-idf 값이 위와 같이 직접한 것과 다른 이유

scikit-learn 에서의 idf 구하는 식이 다음과 같다.
$\log{\left(\frac{1+n}{1+df}\right)}$
위에서 배운 식과 다르게 분자에도 1을 더해줌을 알 수 있다.

뿐만아니라 tf-idf를 구할 떄에도 tf와 idf를 바로 곱하는 것이 아니라, idf에 1을 더하여 계산한다.
$tfidf=tf \times (idf+1)$
여기서 왜 idf에 1을 더해주는지는 잘 모르겠다.

마지막으로 여기에 L2 norm이란 걸 해준다고 한다. L2 norm 간단히 말하면 X라는 벡터의 각 원소들을 제곱합에 루트를 씌워준다.
$\sqrt{\sum_{k=1}^N x_k^2} \quad where . \quad X=[x_1,x_2,x_3, ..., x_n]$
이 값을 각 원소에 나눠서 tf-idf 값을 결정한다.
$tfidf = x_1 / \sqrt{\sum_{k=1}^N x_k^2}$

reference

• https://m.blog.naver.com/duqrlwjddns1/221780750830

개요

오늘도 딥 러닝을 이용한 자연어 처리 입문 교재를 가지고 공부를 한다.
텍스트 전처리 다음으로 두번째로 공부할 내용은 언어모델이다. 언제 20 챕터까지...

느려도 좋으니 끝까지 할 수 있었으면 좋겠다.. 😂

1. 언어모델

언어 모델(Languagel Model)이란 단어 시퀀스(문장)에 확률을 할당하는 모델을 말한다. 어떤 문장들이 있을 때, 적절한지 사람처럼 판단할 수 있다면, 기계가 자연어 처리를 정말 잘 한다고 볼 수 있다. 이게 바로 언어 모델이 하는 일이다.

1.1 주어진 이전 단어들로부터 다음 단어 예측하기

확률을 할당하게 하기 위해서 가장 보편적으로 사용되는 방법은 언어 모델이 이전 단어들이 주어졌을 때 다음 단어를 예측하도록 하는 것이다.

1.1.1 단어 시퀀스의 확률

하나의 단어를 w, 단어 시퀀스을 대문자 W라고 한다면, n개의 단어가 등장하는 단어 시퀀스 W의 확률은 다음과 같다. P는 확률

$P(W)=P(w_1,w_2,w_3,w_4,w_5,...,w_n)$

1.1.2 다음 단어 등장 확률

n-1개의 단어가 나열된 상태에서 n번째 단어의 확률은 다음과 같다.

$P(w_n|w_1,...,w_{n−1})$

|의 기호는 조건부 확률(conditional probability)을 의미한다. * 참고 : $P(B|A) = \frac{P(A\cap B)}{P(A)}$

전체 단어 시퀀스 W의 확률은 모든 단어가 예측되고 나서야 알 수 있으므로 단어 시퀀스의 확률은 다음과 같다.

$P(W)=P(w_1,w_2,w_3,w_4,w_5,...w_n)=\prod_{i=1}^n P(w_n|w_1,...,w_{n−1})$

$\prod_{i=1}^n$ 는 곱기호로 요소들을 전부 곱한다는 뜻이다.

1.2 언어 모델 직관적으로 이해해보기

비행기를 타려고 공항에 갔는데 지각을 하는 바람에 비행기를 [ ] 라는 문장이 있다. 빈 괄호 안에 올 단어가 사람은 쉽게 '놓쳤다'라고 예상할 수 있다. 우리 지식에 기반하여 나올 수 있는 여러 단어들을 후보에 놓고 놓쳤다는 단어가 나올 확률이 가장 높다고 판단하였기 때문이다.

그렇다면 기계에게 위 문장을 주고, '비행기를' 다음에 나올 단어를 예측해보라고 한다면 과연 어떻게 최대한 정확히 예측할 수 있을까? 기계도 비슷하다. 앞에 어떤 단어들이 나왔는지 고려하여 후보가 될 수 있는 여러 단어들에 대해서 등장 확률을 추정하고 가장 높은 확률을 가진 단어를 선택한다.

ex. 검색엔진 같은경우 검색시 다음 단어를 예측해서 추천해준다.

2. 통계적 언어 모델(Statistical Language Model, SLM)

언어 모델의 전통적인 접근 방법인 통계적 언어 모델이다.

2.1 문장에 대한 확률

위에서 잠깐 언급 됐던, 조건부 확률의 연쇄 법칙을 이용해 문장의 확률을 구해보자.

➕ 연쇄 법칙(chain rule)

$P(x_1,x_2,x_3...x_n)=P(x_1)P(x_2|x_1)P(x_3|x_1,x_2)...P(x_n|x_1...x_{n−1})$

이 조건부확률을 이용하여 '안녕하세요 저는 딥러닝을 공부하고 있습니다.' 라는 문장의 확률을 구해보자.

이것을 수식으로 표현 한다면 다음과 같다.

P(안녕하세요 저는 딥러닝을 공부하고 있습니다.) = P(안녕하세요) x P(저는|안녕하세요) x
P(딥러닝을|안녕하세요 저는) x ... x P(있습니다.|안녕하세요 저는 딥러닝을 공부하고)

말로 풀어본다면, 해당 문장의 확률은
'안녕하세요'가 나올 확률 X
'안녕하세요'가 나오고 '저는'이 나올 확률 X
'안녕하세요 저는'이 나오고 '딥러닝을'이 나올확률 X ... X
'안녕하세요 저는 딥러닝을 공부하고 있습니다.'가 나오고 '있습니다'가 나올 확률 이다.

결론은 문장의 확률을 구하기 위해서 각 단어에 대한 예측 확률들을 곱한다.

2.2 카운트 기반의 접근

문장의 확률을 구하기 위해 각 단어에 대한 예측 확률을 모두 곱한다는 것은 알겠지만 이전 단어로부터 다음 단어에 대한 확률은 어떻게 구할까? 그것은 바로, 카운트에 기반하여 확률을 계산한다.

'안녕하세요 저는 딥러닝을 공부하고'가 나왔을 때 '있습니다'가 나올 확률을 구해보자

$P(있습니다|안녕하세요 저는 딥러닝을 공부하고) = \frac{count(안녕하세요 저는 딥러닝을 공부하고 있습니다)}{count(안녕하세요 저는 딥러닝을 공부하고)}$

단순히 학습한 코퍼스 데이터에서 '안녕하세요 저는 딥러닝을 공부하고'가 100번 등장하고, 그 다음에 '있습니다'가 등장한 경우가 30번이라고 한다면 $P(있습니다|안녕하세요 저는 딥러닝을 공부하고)$ 는 30%가 된다.

➕ 카운터 기반의 한계 - 희소 문제(Sparsity Problem)

기계에게 많은 코퍼스를 훈련시켜서 언어 모델을 통해 현실에서의 확률 분포를 근사하는 것이 언어 모델의 목표이다. 하지만, 카운트 기반으로 접근하려고 한다면 갖고있는 코퍼스(corpus). 즉, 다시 말해 기계가 훈련하는 데이터는 정말 방대한 양이 필요하다.

위의 카운트 기반 조건부 확률을 구하는 공식에서 분모에 해당하는 카운트 수가 0이면 확률이 정의될 수가 없다. 쉽게 말해 학습 데이터를 통해 카운트가 한 번도 되지 않거나 아주 적게 되는 경우 언어를 정확히 모델링하지 못하는 문제가 생긴다.

이러한 문제를 완화하기 위해 n-gram이나 스무딩 백오프와 같은 여러가지 일반화(generalization) 기법이 존재한다. 하지만 근본적 해결책은 되지 못하기에, 통계적 언어 모델에서 인공 신경망 언어 모델로 트렌드가 바뀌었다.

3. N-gram 언어 모델(N-gram Language Model)

n-gram 또한 카운트 기반 통계적 접근 언어 모델이므로 SLM의 일종이다. 하지만 모든 단어를 고려하는 것이 아니고, 일부 단어만 고려하는 접근 방법을 사용한다. 이 때 일부 단어를 몇 개 보느냐를 결정하는데 이것이 N-gram의 n 을 의미한다.

3.1 코퍼스에서 카운트하지 못하는 경우를 감소

SLM의 한계는 훈련 코퍼스에 확률을 계산하고 싶은 문장이나 단어가 없을 수 있다는 점이다. 또한 문장이 길어질수록 갖고있는 코퍼스에서 그 문장이 존재하지 않을(카운트할 수 없을) 가능성이 높다. 그런데 다음과 같이 참고하는 단어들을 줄이면 카운트를 할 수 있을 가능성이 높일 수 있다.

가령, An adorable little boy가 나왔을 때 is가 나올 확률을 그냥 boy가 나왔을 때 is가 나올 확률로 생각해보는 건 어떨까? 갖고있는 코퍼스에 An adorable little boy is가 있을 가능성 보다는 boy is라는 더 짧은 단어 시퀀스가 존재할 가능성이 더 높다.

즉, 앞에서는 An adorable little boy가 나왔을 때 is가 나올 확률을 구하기 위해서는 An adorable little boy가 나온 횟수와 An adorable little boy is가 나온 횟수를 카운트해야만 했지만, 이제는 단어의 확률을 구하고자 기준 단어의 앞 단어를 전부 포함해서 카운트하는 것이 아니라, 앞 단어 중 임의의 개수만 포함해서 카운트하여 근사하자는 것이다. 이렇게 하면 갖고 있는 코퍼스에서 해당 단어의 시퀀스를 카운트할 확률이 높아집니다.

3.2 N-gram

예를 들어 '안녕하세요 저는 딥러닝을 공부하고 있습니다.' 라는 문장에 대해 n-gram을 전부 구해보면 아래와 같다.

unigrams : 안녕하세요 / 저는 / 딥러닝을 / 공부하고 / 있습니다.
bigrams : 안녕하세요 저는 / 저는 딥러닝을 / 딥러닝을 공부하고 / 공부하고 있습니다.
trigrams : 안녕하세요 저는 딥러닝을 / 저는 딥러닝을 공부하고 / 딥러닝을 공부하고 있습니다.
4-grams : 안녕하세요 저는 딥러닝을 공부하고 / 저는 딥러닝을 공부하고 있습니다.

n-gram을 통한 언어 모델에서는 다음에 나올 단어의 예측은 오직 n-1개의 단어에만 의존한다. 예를 들어 '안녕하세요 저는 딥러닝을 공부하고' 다음에 나올 단어를 예측하고 싶다고 할 때, n=3 라고 한 3-gram을 이용한 언어 모델을 사용한다고 합시다. 이 경우, 공부하고 다음에 올 단어를 예측하는 것은 다른 부분은 제외한 n-1에 해당되는 앞의 2개의 단어(예제에서 '딥러닝을 공부하고')만을 고려합니다.

3.3 N-gram의 한계

예를 들어서 '골목에서 담배를 피던 소녀가 나를 쳐다봐서 [ ].' 라는 문장의 마지막에 들어갈 단어를 정하는데, 4-gram 이라 가정한다면 소녀가 나를 쳐다봐서 '설레였다' 라는 문장이 카운트가 많이 되서 결정 될 수 있다는 점이다. 근처 단어 몇 개만 고려하니, 문장 앞쪽의 '골목에서 담배를 피던'이란 수식어가 반영이 되지 않아 '무서웠다'와 같이 의도하고 싶은 대로 문장을 끝맺음하지 못하는 경우가 생긴다는 점이다. 뿐만아니라 여전히 카운트를 기반으로 하기때문에 희소 문제가 존재한다.

➕ n 을 선택하는 것은 trade-off 문제

trade-off 란, 질과 량 가운데 어느 한편을 늘리면 다른 한편은 그 만큼 줄어드는 것을 이르는 말이다.
혹시나 나처럼 trade-off의 뜻을 모르는 분들을 위해 적어둔다.

n을 크게하면 실제 훈련 코퍼스에서 해당 n-gram을 카운트할 수 있는 확률은 적어지므로 희소 문제는 점점 심각해지고, 모델 사이즈가 커진다는 문제점도 있다. 기본적으로 코퍼스의 모든 n-gram에 대해서 카운트를 해야 하기 때문이다.

n을 작게 선택하면 훈련 코퍼스에서 카운트는 잘 되겠지만 근사의 정확도는 현실의 확률분포와 멀어진다. 그렇기 때문에 적절한 n을 선택해야 합니다. 앞서 언급한 trade-off 문제로 인해 정확도를 높이려면 n은 최대 5를 넘게 잡아서는 안 된다고 권장되고 있다.

그래도 n을 1보다는 2로 선택하는 것은 거의 대부분의 경우에서 언어 모델의 성능을 높일 수 있다.

4. 한국어에서의 언어 모델

영어나 기타 언어에 비해 한국어는 정말 까다롭다. 대표적인 이유를 살펴보자.

4.1 한국어는 어순이 중요하지 않다.

ex) 떡볶이 진짜 맛있지 않냐? = 진짜 맛있지 않냐 떡볶이?
어순이 중요하지 않다는 것은, 어떤 단어든 나타나도 된다는 의미이다. 언어 모델이 얼마나 헷갈릴까..

4.2 한국어는 교착어다.

한국어는 조사와 같은 것이 있어 발생가능한 단어 수를 굉장히 늘린다.
ex) '그녀' => 그녀가, 그녀를, 그녀의, 그녀로, 그녀에게, 그녀처럼 등 다양한 경우 존재.

그래서 한국어에서는 토큰화를 통해 접사나 조사 등을 분리하는 것이 중요한 작업이 되기도 한다.

4.3 한국어는 띄어쓰기가 제대로 지켜지지 않는다.

한국어는 띄어쓰기를 제대로 하지 않아도 의미가 전달되며, 띄어쓰기 규칙 또한 상대적으로 까다로운 언어이기 때문에 한국어 코퍼스는 띄어쓰기가 제대로 지켜지지 않는 경우가 많다. 토큰이 제대로 분리 되지 않는채 훈련 데이터로 사용된다면 언어 모델은 제대로 동작하지 않습니다.

5. 펄플렉서티(Perplexity)

두 개의 모델 A, B가 있을 때 이 모델의 성능은 어떻게 비교할 수 있을까? 일일히 모델들에 대해서 실제 작업을 시켜보고 정확도를 비교하는 작업은 공수가 너무 많이 드는 작업이다.

이러한 평가를 외부 평가(extrinsic evaluation)라고 하는데, 이러한 평가보다는 어쩌면 조금은 부정확할 수는 있어도 테스트 데이터에 대해서 빠르게 식으로 계산되는 더 간단한 평가 방법이 있다. 바로 모델 내에서 자신의 성능을 수치화하여 결과를 내놓는 내부 평가(Intrinsic evaluation)에 해당되는 펄플렉서티(perplexity)이다.

5.1 언어 모델의 평가 방법(Evaluation metric) : PPL

펄플렉서티(perplexity)는 언어 모델을 평가하기 위한 내부 평가 지표이고, 보통 줄여서 PPL이 라고 표현한다. 'perplexed'라는 '헷갈리는'과 유사한 의미가져서 그런가 PPL은 수치가 높으면 좋은 성능을 의미하는 것이 아니라, '낮을수록' 언어 모델의 성능이 좋다는 것을 의미한다.

PPL은 단어의 수로 정규화(normalization) 된 테스트 데이터에 대한 확률의 역수이다.PPL을 최소화한다는 것은 문장의 확률을 최대화하는 것과 같다. 문장 W의 길이가 N이라고 할 때 다음과 같다.

$PPL(W) = P(w_1,w_2,w_3, ... ,w_N)^{-\frac{1}{N}} = \sqrt[N]{\frac{1}{P(w_1,w_2,w_3, ... ,w_N)}}$

문장의 확률에 연쇄 법칙을 적용 하면,

$PPL(W) = \sqrt[N]{\frac{1}{P(w_1,w_2,w_3, ... ,w_N)}} = \sqrt[N]{\frac{1}{\prod_{i=1}^N P(w_i|w_1,...,w_{i−1})}}$

n-gram까지 적용이 되면, ex. bigram

$PPL(W) = \sqrt[N]{\frac{1}{\prod_{i=1}^N P(w_i|w_{i−1})}}$

5.2 분기 계수 (Branching factor)

PPL은 선택할 수 있는 가능한 경우의 수를 의미하는 분기계수(branching factor)이다. PPL은 이 언어 모델이 특정 시점에서 평균적으로 몇 개의 선택지를 가지고 고민하고 있는지를 의미한다. 어떤 테스트 데이터을 주고 측정했더니 PPL이 10이 나왔다고 해보자.

$PPL(W) = P(w_1,w_2,w_3, ... ,w_N)^{-\frac{1}{N}} = (\frac{1}{10}^{N})^{-\frac{1}{N}} = \frac{1}{10}^{-1} = 10$

같은 테스트 데이터에 대해서 두 언어 모델의 PPL을 각각 계산 후에 PPL의 값을 비교하면, 두 언어 모델 중 어떤 것이 성능이 좋은지도 판단이 가능합니다.

주의할 점은 PPL의 값이 낮다는 것은 테스트 데이터 상에서 높은 정확도를 보인다는 것이지, 사람이 직접 느끼기에 좋은 언어 모델이라는 것을 반드시 의미하진 않는다는 점이다. 또한 언어 모델의 PPL은 테스트 데이터에 의존하므로 두 개 이상의 언어 모델을 비교할 때는 정량적으로 양이 많고, 또한 도메인에 알맞은 동일한 테스트 데이터를 사용해야 신뢰도가 높다는 것이다.

개요

살다보니 생각보다 자연어처리가 재밌기도 하고, 실제로도 많이 이용하게 되는 것 같아서 지대로 공부를 해보고 싶어졌다. 너무 수박 겉핥기 식으로만 알고 있었던 것 같아서 하나씩 정리하면서 차근차근 공부해보자! 원래는 종이 책을 하나 뗄까도 싶었지만, 페이지 넘기는 것도 귀찮기에 갓키독스(wikidocs)에 있는 갓(유)원준님의 딥러닝을 이용한 자연어 처리 입문으로 정했다! 예제도 잘 되어있어서 정말 좋다!

그럼 하나씩 정독하면서 중요한 부분을 정리하면서 내 생각과 이해한 것을 적어보도록 하자~~😆

시작하기에 앞서, 전처리란?!

자연어 처리에서 크롤링 등으로 얻어낸 코퍼스 데이터를 필요에 맞게 사용하기 위해서는 전처리를 진행해야 한다. 요리로 비유를 하자면, 재료를 날 것 그대로 사용한다면 맛을 보장할 수 없을 것이다. 우리는 성능을 보장할 수 없지 않겠는가? 그렇다면 어떻게 해야할까. 데이터를 용도에 맞게 사용하고자 토큰화, 정제, 정규화를 진행해야 한다.

1. 토큰화(Tokenization)

첫번째 토큰화는 주어진 코퍼스(corpus)에서 토큰(token)이라 불리는 단위로 나누는 작업을 토큰화라고 한다. 이 토큰의 단위는 상황에 따라 다르지만, 보통 의미있는 단위로 토큰을 정의한다.

* 토큰화에서 고려해야할 사항

토큰화 작업을 단순하게 코퍼스에서 구두점을 제외하고 공백 기준으로 잘라내는 작업이라고 간주할 수는 없다. 그 이유에 대해 살펴보자.

1. 구두점이나 특수 문자를 단순 제외할 때
   • ex. 21/02/06 -> 날짜 , $100,000 -> 돈을 나타낼 때
2. 줄임말과 단어 내 띄어쓰기
   • ex. we're -> we are 의 줄임말./ rock n roll -> 하나의 단어지만 띄어쓰기가 존재.
3. 문장 토큰화 : 단순 마침표를 기준으로 자를 수 없음.
   • ex. IP 192.168.56.31 서버에 들어가서 로그 파일 저장해서 ukairia777@gmail.com로 결과 좀 보내줘. 그러고나서 점심 먹으러 가자.

* 한국어 토큰화의 어려움

영어는 New York과 같은 합성어나 he's 와 같이 줄임말에 대한 예외처리만 한다면, 띄어쓰기(whitespace)를 기준으로 하는 띄어쓰기 토큰화를 수행해도 단어 토큰화가 잘 작동한다.

• 영어와는 달리 한국어에는 조사라는 것이 존재
  • ex. '그가', '그에게', '그를', '그와', '그는'과 같이 다양한 조사가 붙음. 같은 단어임에도 서로 다른 조사가 붙어서 다른 단어로 인식이
• 한국어는 띄어쓰기가 영어보다 잘 지켜지지 않는다.
  • ex. 띄어쓰기를안해도사람들은이해를합니다.

🤔 그럼 어쩌란거지?

한국어 토큰화에서는 형태소(morpheme)란 뜻을 가진 가장 작은 말의 단위인 이 개념을 반드시 이해해야 한다. 이 형태소에는 두 가지 형태소가 있는데 자립 형태소와 의존 형태소가 존재 한다.

1. 자립 형태소 : 접사, 어미, 조사와 상관없이 자립하여 사용할 수 있는 형태소. 그 자체로 단어가 된다. 체언(명사, 대명사, 수사), 수식언(관형사, 부사), 감탄사 등이 있다.
2. 의존 형태소 : 다른 형태소와 결합하여 사용되는 형태소. 접사, 어미, 조사, 어간를 말한다.

• ex. 문장 : 에디가 딥러닝책을 읽었다.
  1. 자립 형태소 : 에디, 딥러닝책
  2. 의존 형태소 : -가, -을, 읽-, -었, -다

한국어 토큰화를 도와주는 형태소 분석기

konlpy의 Kkma, Okt, mecab 또는 Pykomoran 등이 있다. 형태소 분석기 마다 성능이 다르기에 결과가 다르다.

• 대표적 형태소 분석기의 기능
  1) morphs : 형태소 추출
  2) pos : 품사 태깅(Part-of-speech tagging)
  3) nouns : 명사 추출

3가지 분석기의 형태소 추출(morphs)를 실행했는데 시간도 다르고 결과도 다른 것을 알 수 있다. 그렇기에 필요 용도에 따라 적절한 분석기를 사용하면 된다. 예시에는 없지만 속도가 중요하다면 mecab을 이용할 수 있다.

2. 정제(Cleaning)와 정규화(Normalization)

토큰화 작업 전, 후에는 텍스트 데이터를 용도에 맞게 정제 및 정규화하는 일이 항상 함꼐한다. 목적은 다음과 같다.

1. 정제 : 갖고 있는 코퍼스로부터 노이즈 데이터를 제거한다.
2. 정규화 : 표현 방법이 다른 단어들을 통합시켜서 같은 단어로 만들어준다.

2.1 정제(Cleaning)

2.1.1 정규 표현식(Regular Expression)

• 얻어낸 코퍼스에서 노이즈 데이터의 특징 및 패턴을 잡아낼 수 있다면, 정규 표현식을 통해서 이를 제거할 수 있는 경우가 많다. 코퍼스 내에 계속해서 등장하는 글자들을 규칙에 기반하여 한 번에 제거하는 방식으로서 사용 가능.
  ex. 뉴스 기사를 크롤링 -> 기사 게재 시간 등

2.1.2 불필요한 단어 제거 (Removing Unnecessary Words)

자연어가 아니면서 아무 의미도 갖지 않는 글자들(특수 문자 등) 뿐만아니라 분석하고자 하는 목적에 맞지 않는 불필요 단어들을 노이즈 데이터라고 하기도 한다.

1. 등장 빈도가 적은 단어
   • ex. 100,000개의 메일 데이터에서 총 합 5번 밖에 등장하지 않은 단어의 경우 직관적으로 분류에 거의 도움이 되지 않을 것
2. 길이가 짧은 단어(Removing words with very a short length)
   영어는 길이가 2~3 이하인 단어를 제거하는 것만으로도 크게 의미를 갖지 못하는 단어를 줄이는 효과를 갖고 있지만, 한국어 단어는 한자어가 많고, 한 글자만으로도 이미 의미를 가진 경우가 많다
   • ex. 영어 : 2~3 글자 이하 it, at, to, on, in, by 불용어 제거 가능.
     한국어 : 용(龍) 한국어로는 한 글자 영어에서는 d, r, a, g, o, n 6글자.

➕ 한국어에서 불용어 제거하기

간단하게는 토큰화 후에 조사, 접속사 등을 제거하기. 조사나 접속사와 같은 단어들뿐만 아니라 명사, 형용사와 같은 단어들 중에서 불용어로서 제거하고 싶은 단어들이 생기기도 한다. 결국에는 사용자가 직접 불용어 사전을 만들게 되는 경우가 많다.

• 예를 들어 문장에서 의도를 파악하는 것을 하려고 할 때

from konlpy.tag import Okt, Kkma, Komoran
okt=Okt()

text='시원한 콜라, 그리고 맛있는 햄버거 포장해 주세요.'
stop_words=['시원한', '맛있는', '그리고', '해', '주세요', ',', '.']

word_token = okt.morphs(text)
print(word_token)
# ['시원한', '콜라', ',', '그리고', '맛있는', '햄버거', '포장', '해', '주세요', '.']

result=[]
for word in word_token:
    if word not in stop_words:
        result.append(word)

print(result)
# ['콜라', '햄버거', '포장']

2.2 정규화(Normalization)

규칙에 기반한 표기가 다른 단어들의 통합을 생각해 볼 수 있다. 종류에는 어간 추출(stemming)과 표제어 추출(lemmatizaiton) 등이 있다. 자연어 처리에서 전처리, 더 정확히는 정규화의 지향점은 언제나 갖고 있는 코퍼스로부터 복잡성을 줄이는 일이다.

➕ 형태소의 두 가지 종류 : 어간(stem)과 접사(affix)

1) 어간(stem) : 단어의 의미를 담고 있는 단어의 핵심 부분.
2) 접사(affix) : 단어에 추가적인 의미를 주는 부분. ex. cat(어간)와 -s(접사)

2.2.1 표제어 추출(Lemmatization)

한글로는 '표제어' 또는 '기본 사전형 단어' 정도의 의미

• ex. am, are, is는 서로 다른 스펠링이지만 그 뿌리 단어인 be는 이 단어들의 표제어라고 할 수 있다.

2.2.2 어간 추출(Stemming)

어간 추출은 형태학적 분석을 단순화한 버전, 정해진 규칙만으로 단어의 어미를 자르는 어림짐작의 작업이라고 볼 수도 있다.

• ex. formalize → formal / allowance → allow / electricical → electric 이와 같이 단순 어미 자름.

한국어에서의 어간 추출 : 용언에 해당되는 '동사'와 '형용사'는 어간(stem)과 어미(ending)의 결합으로 구성

➕ 활용(conjugation) : 용언의 어간(stem)이 어미(ending)를 가지는 일을 말한다.

1. 규칙활용 : 어간의 모습이 일정.
   ex. 잡/어간 + 다/어미
2. 불규칙활용 : 어간이나 어미의 모습이 변함. 단순한 분리만으로 어간 추출이 되지 않고 좀 더 복잡한 규칙을 필요로 함.
   ex. ‘듣-, 돕-, 곱-, 잇-, 오르-, 노랗-’ 등이 ‘듣/들-, 돕/도우-, 곱/고우-, 잇/이-, 올/올-, 노랗/노라-’와 같이 어간의 형식이 달라지는 일이 있거나 ‘오르+ 아/어→올라, 하+아/어→하여, 이르+아/어→이르러, 푸르+아/어→푸르러’와 같이 일반적인 어미가 아닌 특수한 어미를 취하는 경우

➕ 한국어 자연어처리 파이썬 라이브러리 soynlp의 normalization

from soynlp.normalizer import *

emoticon_normalize('ㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋ쿠ㅜㅜㅜㅜㅜㅜ', num_repeats=3)
# 'ㅋㅋㅋㅜㅜㅜ'

repeat_normalize('와하하하하하하하하하핫', num_repeats=2)
# '와하하핫'

only_hangle('가나다ㅏㅑㅓㅋㅋ쿠ㅜㅜㅜabcd123!!아핫')
# '가나다ㅏㅑㅓㅋㅋ쿠ㅜㅜㅜ 아핫'

only_hangle_number('가나다ㅏㅑㅓㅋㅋ쿠ㅜㅜㅜabcd123!!아핫')
# '가나다ㅏㅑㅓㅋㅋ쿠ㅜㅜㅜ 123 아핫'

only_text('가나다ㅏㅑㅓㅋㅋ쿠ㅜㅜㅜabcd123!!아핫')
# '가나다ㅏㅑㅓㅋㅋ쿠ㅜㅜㅜabcd123!!아핫'

3. 정수 인코딩(Integer Encoding)

컴퓨터는 텍스트보다는 숫자를 더 잘 처리 할 수 있다. 이를 위해 텍스트를 숫자로 바꾸는 여러가지 기법들이 있다. 그 전에 첫 단계로 각 단어를 고유한 정수에 맵핑(mapping)시키는 전처리 작업이 필요할 때가 있다. 인덱스를 부여하는 방법은 랜덤으로 부여하기도 하지만, 보통은 전처리 또는 단어 빈도수를 기준으로 정렬한 뒤에 부여한다.
ex. 텍스트에 단어가 5,000개 존재시 각각 1번부터 5,000번까지 단어와 맵핑되는 고유한 정수, 다른 표현으로는 인덱스를 부여. 가령, book은 150번, dog는 171번과 같이 숫자가 부여

결론 : 컴퓨터가 알아먹기 쉽게 바꿔주는 것!

➕ 실습해보기

단어에 정수를 부여하는 방법 중 하나로 단어를 빈도수 순으로 정렬한 단어 집합(vocabulary)을 만들고, 빈도수가 높은 순서대로 차례로 낮은 숫자부터 정수를 부여하는 방법이 있다. 구현하는 방법은 다양하다.

1. dictionary 사용하기
2. 내장 모듈 Counter 사용하기
3. 내장 함수 enumerate 사용하기
4. Keras Tokenizer 사용하기

>> 예제 코드 보러가기

4. 패딩(Padding)

자연어 처리를 하다보면 문장(또는 문서)의 길이가 서로 다를 수 있다. 그런데 기계는 길이가 전부 동일한 문서들에 대해서는 하나의 행렬로 보고, 한꺼번에 묶어서 처리할 수 있다. 다시 말해 병렬 연산을 위해서 여러 문장의 길이를 임의로 동일하게 맞춰주는 작업이 필요할 때가 있다.

쉽게 말해 병렬 연산을 위해 문장(또는 문서)의 길이를 동일하게 맞춰 주는 작업이다. 길면 자르고, 짧으면 특정 값으로 채워준다.

➕ 실습해보기

패딩을 할 때 가장 긴 길이를 가진 문서의 길이를 기준으로 패딩을 한다고 능사는 아니다. 가령, 모든 문서의 평균 길이가 20인데 문서 1개의 길이가 5,000이라고 해서 굳이 모든 문서의 길이를 5,000으로 패딩할 필요는 없을 수 있다. 반대로 너무 짧게 잡으면 잘려나가는 데이터들이 많이 존재하므로, 문서 길이의 분포를 보고 결정하는 것이 좋다.

1. Numpy로 패딩
2. Keras 전처리 도구로 패딩

>> 예제 코드 보러가기

5. 원-핫 인코딩(One-Hot Encoding)

단어 집합의 크기를 벡터의 차원으로 하고, 표현하고 싶은 단어의 인덱스에 1의 값을 부여하고, 다른 인덱스에는 0을 부여하는 단어의 벡터 표현 방식입니다. 두 가지 과정으로 정리 할 수 있다. 1) 정수 인코딩 2) 해당 단어 1부여, 나머지 0부여

➕ 예제

label = ['한식', '중식', '일식', '양식']
word2index={}
for idx, word in enumerate(label):
    word2index[word]=idx

print(word2index)
# {'한식' : 0, '중식' : 1, '일식' : 2, '양식' : 3}

정수 인코딩을 진행한 후,

# 원-핫 인코딩 함수 정의
def one_hot_encoding(word, word2index):
    one_hot_vector = [0]*(len(word2index))
    index=word2index[word]
    one_hot_vector[index]=1
    return one_hot_vector

vec=one_hot_encoding("한식",word2index)
print(vec)
# [1,0,0,0]

또는 Keras 의 to_categorical을 이용해서 정수 인코딩 된 리스트를 인풋으로 넣으면 쉽게 얻을 수 있다.

from tensorflow.keras.utils import to_categorical

# 아까 한식중식 정수 인코딩 된 것.
encoded=[0,1,2,3]
one_hot = to_categorical(encoded)
print(one_hot)
#[[1, 0, 0, 0] #인덱스 0의 원-핫 벡터
#[0, 1, 0, 0] #인덱스 1의 원-핫 벡터
#[0, 0, 1, 0] #인덱스 2의 원-핫 벡터
#[0, 0, 0, 1]] #인덱스 3의 원-핫 벡터

원-핫 인코딩의 한계

1. 단어의 개수가 늘어날 수록, 벡터를 저장하기 위해 필요한 공간이 계속 늘어난다는 단점
   • ex. 단어 1000개일 경우 1의 값을 가지는 1개 빼곤 999개의 값은 0을 가짐.
2. 단어 유사도 표현 못함.

이를 보완하기 위한 벡터화 기법

1. 카운트 기반의 벡터화 방법 : LSA, HAL 등
2. 예측 기반으로 벡터화 방법 : NNLM, RNNLM, Word2Vec, FastText 등
3. 두 가지 방법을 모두 사용 : GloVe

⚖️ 데이터의 분리 (Splitting Data)

이 파트는 머신 러닝(딥 러닝) 모델에 데이터를 훈련시키기 위해 데이터를 분리하는 작업은 꼭 필요하기에 남겨두었다. 기본적이지만 모르면 안되는 부분이기에 혹시나 유용히 쓰이는 것이 있을 수 있다.

1️⃣ X,Y 분리하기

1. zip 함수 이용

sequences=[['a', 1], ['b', 2], ['c', 3]] # 리스트의 리스트 또는 행렬 또는 2D 텐서.
X,y = zip(*sequences)
# 또는 (위 아래 결과 똑같음)
X,y = zip(['a', 1], ['b', 2], ['c', 3])

print(X) # ('a', 'b', 'c')
print(y) # (1, 2, 3)

2. pandas 데이터프레임 이용

import pandas as pd

values = [['당신에게 드리는 마지막 혜택!', 1],
['내일 뵐 수 있을지 확인 부탁드...', 0],
['도연씨. 잘 지내시죠? 오랜만입...', 0],
['(광고) AI로 주가를 예측할 수 있다!', 1]]
columns = ['메일 본문', '스팸 메일 유무']

df = pd.DataFrame(values, columns=columns)
X=df['메일 본문']
Y=df['스팸 메일 유무']
print(X) # ['당신에게 드리는 마지막 혜택!', '내일 뵐 수 있을지 확인 부탁드...', ...]
print(Y) # [1, 0, 0, 1]

3. numpy 이용

import numpy as np
ar = np.arange(0,16).reshape((4,4))
print(ar)
# [[ 0  1  2  3]
# [ 4  5  6  7]
# [ 8  9 10 11]
# [12 13 14 15]]

X=ar[:, :3]
y=ar[:,3]
print(X) # [[ 0  1  2], [ 4  5  6], [ 8  9 10], [12 13 14]]
print(y) # [3 7 11 15]

2️⃣ 테스트 데이터 분리하기

이건 정말 필요하다. 이미 분리된 X,y 셋에서 어느정도 비율을 가지고 훈련 셋과 테스트 셋을 분리할 떄 유용하다.

1. scikit-learn 이용하기

# test_size에 테스트 셋을 몇 퍼센트 넣을 것인지 지정해준다. ex) 0.2 => 8:2 비율로 나누겠다.
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size= 0.2, random_state=1234)

2. 직접 분리하기

import numpy as np
X, y = np.arange(0,24).reshape((12,2)), range(12)
# 실습을 위해 임의로 X와 y가 이미 분리 된 데이터를 생성

# 몇개까지 자를 건지 지정
n_of_train = int(len(X) * 0.8) # 데이터의 전체 길이의 80%에 해당하는 길이값을 구한다.
n_of_test = int(len(X) - n_of_train) # 전체 길이에서 80%에 해당하는 길이를 뺀다.
print(n_of_train) # 9
print(n_of_test) # 3

# 위의 값 기준으로 자르기.
X_test = X[n_of_train:] #전체 데이터 중에서 20%만큼 뒤의 데이터 저장
y_test = y[n_of_train:] #전체 데이터 중에서 20%만큼 뒤의 데이터 저장
X_train = X[:n_of_train] #전체 데이터 중에서 80%만큼 앞의 데이터 저장
y_train = y[:n_of_train] #전체 데이터 중에서 80%만큼 앞의 데이터 저장

reference

• https://wikidocs.net/21698
• https://github.com/lovit/soynlp